গণিত

বিখ্যাত গ্রিক গণিতবিদ পীথাগোরাস (৫৭০-৪৯৫ খ্রিষ্টপূর্ব)

গণনা করা ছিল আদিমতম গাণিতিক কর্মকাণ্ড। আদিম মানুষেরা পশু ও বাণিজ্যের হিসাব রাখতে গণনা করত। আদিম সংখ্যা ব্যবস্থাগুলি প্রায় নিশ্চিতভাবেই ছিল এক বা দুই হাতের আঙুল ব্যবহার করে সৃষ্ট। বর্তমানের ৫ ও ১০-ভিত্তিক সংখ্যা ব্যবস্থার বিস্তার এরই সাক্ষ্য দেয়। মানুষ যখন সংখ্যাগুলিকে বাস্তব বস্তু থেকে পৃথক ধারণা হিসেবে গণ্য করা শিখল এবং যোগ, বিয়োগ, গুণ, ভাগ --- এই চারটি মৌলিক অপারেশন বা প্রক্রিয়া উদ্ভাবন করল, তখনই পাটীগণিতের যাত্রা শুরু হল। আর জ্যামিতির শুরু হয়েছিল রেখা ও বৃত্তের মত সরল ধারণাগুলি দিয়ে। গণিতের পরবর্তী উন্নতির জন্য চলে যেতে হবে খ্রিস্টপূর্ব ২০০০ অব্দে, যখন ব্যাবিলনীয় ও মিশরীয় সভ্যতা বিকাশ লাভ করেছিল।

প্রাচীন মেসোপটেমিয়ার ব্যাবিলনীয়রা এবং নীল নদের অববাহিকায় প্রাচীন মিশরীয়রা সুশৃঙ্খল গণিতের প্রাচীনতম নিদর্শন রেখে গেছে। তাদের গণিতে পাটীগণিতের প্রাধান্য ছিল। জ্যামিতিতে পরিমাপ ও গণনাকে প্রাধান্য দেয়া হয়, স্বতঃসিদ্ধ বা প্রমাণের কোন নিদর্শন এগুলিতে পাওয়া যায় না।

ব্যাবিলনিয়ার গণিত সম্পর্কে আমরা জানতে পারি এই সভ্যতার নিদর্শনবাহী কাদামাটির চাঙড় থেকে, যেগুলির উপর ব্যাবিলনীয়রা কীলক আকৃতির খোদাই করে করে লিখত। এই লেখাগুলিকে কিউনিফর্ম বলা হয়। সবচেয়ে প্রাচীন চাঙড়গুলি খ্রিস্টপূর্ব ৩০০০ অব্দ সালের বলে ধারণা করা হয়। খোদাইগুলির বেশির ভাগ গণিতই ছিল বাণিজ্য বিষয়ক। ব্যাবিলনীয়রা অর্থ ও পণ্যদ্রব্য আদানপ্রদানের জন্য পাটীগণিত ও সরল বীজগণিত ব্যবহার করত। তারা সরল ও যৌগিক সুদ গণনা করতে পারত, কর গণনা করতে পারত, এবং রাষ্ট্র, ধর্মালয় ও জনগণের মধ্যে সম্পদ কীভাবে বন্টিত হবে তা হিসাব করতে পারত। খাল কাটা, শস্যাগার নির্মাণ ও অন্যান্য সরকারি কাজকর্মের জন্য পাটীগণিত ও জ্যামিতির ব্যবহার হত। শস্য বপন ও ধর্মীয় ঘটনাবলির জন্য পঞ্জিকা নির্ধারণেও গণিতের ব্যবহার ছিল।

ব্যাবিলনীয় সংখ্যা

বৃত্তকে ৩৬০টি ভাগে বা ডিগ্রীতে বিভক্ত করা এবং প্রতি ডিগ্রী ও মিনিটকে আরও ৬০টি ভাগে বিভক্ত করার রীতি ব্যাবিলনীয় জ্যোতির্বিজ্ঞান থেকে এসেছে। ব্যাবিলনীয়রাই একেক দিনকে ২৪ ঘণ্টায়, প্রতি ঘন্টাকে ৬০ মিনিট ও প্রতি মিনিটকে ৬০ সেকেন্ডে ভাগ করে। তাদের সংখ্যা ব্যবস্থা ছিল ৬০-ভিত্তিক। ১-কে একটি কীলকাকৃতি খাঁজ দিয়ে নির্দেশ করা হত এবং এটি বারবার লিখে ৯ পর্যন্ত নির্দেশ করা হত। ১১ থেকে ৫৯ পর্যন্ত সংখ্যাগুলি ১ এবং ১০-এর জন্য ব্যবহৃত চিহ্ন ব্যবহার করে নির্দেশ করা হত। ৬০-এর চেয়ে বড় সংখ্যার জন্য ব্যাবিলনীয়রা একটি স্থাননির্দেশক চিহ্ন ব্যবহার করত। স্থানিক মানের এই ধারণার উদ্ভাবন গণনাকে অনেক এগিয়ে দেয়। এর ফলে একই প্রতীক বিভিন্ন স্থানে বসিয়ে একাধিক মান নির্দেশ করা সম্ভব হয়। ব্যাবলিনীয়দের সংখ্যা ব্যবস্থায় ভগ্নাংশও নির্দেশ করা যেত। তবে তাদের ব্যবস্থায় শূন্য ছিল না, এবং এর ফলে দ্ব্যর্থতার সৃষ্টি হয়।

ব্যাবিলনীয়রা বিপরীত সংখ্যা, বর্গ সংখ্যা, বর্গমূল, ঘন সংখ্যা ও ঘনমূল, এবং যৌগিক সুদের সারণী প্রস্তুত করেছিল। তারা ২-এর বর্গমূলের একটি ভাল আসন্ন মান নির্ধারণ করতে পেরেছিল। কিউনিফর্ম চাঙড়গুলি থেকে আরও প্রমাণ পাওয়া গেছে যে ব্যাবিলনীয়রা দ্বিঘাত সমীকরণের সমাধানের সূত্র আবিষ্কার করেছিল এবং তারা দশটি অজানা রাশি বিশিষ্ট দশটি সমীকরণের ব্যবস্থা সমাধান করতে পারত।

খিস্টপূর্ব ৭০০ অব্দে এসে ব্যাবিলনীয়রা গণিত ব্যবহার করে চাঁদ ও গ্রহসমূহের গতি নিয়ে গবেষণা আরম্ভ করে। এর ফলে তারা গ্রহগুলির দৈনিক অবস্থান পূর্বাভাসে সক্ষম হয়, যা জ্যোতির্বিজ্ঞান ও জ্যোতিষশাস্ত্র --- দুই ক্ষেত্রেই তাদের কাজে আসে।

গণিতবিদ লিওনার্দ অয়লার (১৭০৭-১৭৮৩), গণিত জনপ্রিয়করনে তাঁর ভূমিকা অবিস্মরনীয়

জ্যামিতিতে ব্যাবিলনীয়রা সদৃশ ত্রিভুজের একই বাহুগুলির মধ্যে সমানুপাতিকতার সম্পর্কের ব্যাপারে অবহিত ছিল। তারা পীথাগোরাসের উপপাদ্য ব্যবহার করে সমস্যা সমাধান করতে পারত এবং অর্ধবৃত্তের উপর অঙ্কিত কোণ যে সমকোণ হয়, তা জানত। তারা সরল সমতলীয় বিভিন্ন চিত্র যেমন সুষম বহুভুজ, ইত্যাদির ক্ষেত্রফলের সূত্র এবং সরল ঘনবস্তুগুলির আয়তনের সূত্র বের করেছিল। তারা পাই-এর জন্য ৩-কে আসন্ন মান হিসেবে ব্যবহার করত।

মিশরীয়রা তাদের স্তম্ভগুলিতে হায়ারোগ্লিফের মাধ্যমে সংখ্যা অঙ্কিত করেছিল, কিন্তু মিশরীয় গণিতের আসল নিদর্শন হল আনুমানিক ১৮০০ খ্রিস্টপূর্বাব্দের দুইটি প্যাপিরাস। এগুলিতে পাটীগণিত ও জ্যামিতির নানা সমস্যা আছে, যার মধ্যে বাস্তব সমস্যা যেমন নির্দিষ্ট পরিমাণ মদ তৈরির জন্য কতটুকু শস্য লাগবে, এক জাতের শস্য ব্যবহার করে মদের যে মান পাওয়া যায়, অন্য জাতের শস্য কতটুকু কাজে লাগিয়ে সেই একই মান পাওয়া যায়, তার সমস্যা।

মিশরীয় বেতন নির্ণয়ে, শস্যক্ষেত্রের ক্ষেত্রফল ও শস্যাগারের আয়তন নির্ণয়ে, কর নির্ণয়ে ও নির্দিষ্ট কাঠামোর জন্য প্রয়োজনীয় ইটের সংখ্যা বের করতে গণিতকে কাজে লাগাত। এছাড়াও পঞ্জিকা গণনাতেও তারা গণিতভিত্তিক জ্যোতির্বিজ্ঞান ব্যবহার করত। পঞ্জিকার সাহায্যে তারা ধর্মীয় ছুটির তারিখ ও নীল নদের বার্ষিক প্লাবনের সময় নির্দেশ করতে পারত।

মিশরীয়দের সংখ্যা ব্যবস্থা ছিল ১০-ভিত্তিক। তারা ১০-এর বিভিন্ন ঘাতের জন্য ভিন্ন ভিন্ন হায়ারোগ্লিফ প্রতীক ব্যবহার করত। তারা ১-এর প্রতীক পাঁচবার লিখে ৫, ১০-এর প্রতীক ৬ বার লিখে ৬০, আর ১০০-র প্রতীক ৩ বার লিখে ৩০০ নির্দেশ করত। একসাথে এই প্রতীকগুলি ৩৬৫ নির্দেশ করত।

১৯০০ খ্রিষ্টাব্দে প্যারিসে অনুষ্ঠিত আন্তর্জাতিক গণিত সম্মেলনে জার্মান গণিতবিদ ডাভিড হিলবের্ট একটি বক্তৃতায় তার তত্ত্বগুলি ব্যাখ্যা করেন। হিলবের্ট গোটিঙেন বিশ্ববিদ্যালয়ের সম্মানসূচক আসনপ্রাপ্ত গণিতবিদ ছিলেন, যে আসনে এর আগে গাউস ও রিমান অধিষ্ঠিত ছিলেন। হিলবের্ট গণিতের প্রায় সমস্ত ক্ষেত্রে অবদান রাখেন। জ্যামিতির ভিত্তি (১৮৯৯) নিয়ে তার ধ্রুপদী গবেষণা যেমন ছিল, তেমনি অন্যান্য গণিতবিদদের সাথে গণিতের ভিত্তি নিয়ে গবেষণাতেও তিনি অবদান রাখেন। প্যারিসের বক্তৃতায় হিলবের্ট ২৩টি গাণিতিক সমস্যা উপস্থাপন করেন এবং তার বিশ্বাস ছিল ২০শ শতকের গাণিতিক গবেষণার উদ্দেশ্য হবে এই সমস্যাগুলির সমাধান খুঁজে বের করা। বাস্তবিকপক্ষেই এই সমস্যাগুলি ২০শ শতকের সিংহভাগ গাণিতিক গবেষণাকর্মের জন্য উদ্দীপক হিসেবে কাজ করেছিল। যখনই কোনও গণিতবিদ একটি করে হিলবের্টের সমস্যার সমাধান খুঁজে পাওয়ার ঘোষণা দিতেন, আন্তর্জাতিক গণিতবিদ সম্প্রদায় অধৈর্যের সাথে সেই সমাধানের বিশদ বিবরণের অপেক্ষায় থাকত।

যদিও উপরের সমস্যাগুলি অত্যন্ত গুরুত্বপূর্ণ ছিল, তা সত্ত্বেও হিলবের্ট একটি ব্যাপার কল্পনায় আনতে পারেন নি, আর তা হল ডিজিটাল প্রোগ্রামযোগ্য গণকযন্ত্র তথা কম্পিউটারের উদ্ভাবন। কম্পিউটার গণিত নিয়ে গবেষণার প্রকৃতি পালটে দেয়। কম্পিউটারের উৎস হিসেবে পাস্কাল ও লাইবনিৎসের গণনাযন্ত্রিকা বা ক্যালকুলেটরকে গণ্য করা হলেও কেবল ১৯শ শতকে এসে ইংরেজ বিজ্ঞানী চার্লস ব্যাবেজ এমন একটি যন্ত্র নকশা করতে সক্ষম হন যা কাগজের টুকরা বা ফিতাতে লেখা নির্দেশমালা অনুসরণ করে স্বয়ংক্রিয়ভাবে গাণিতিক ক্রিয়া সম্পাদন করতে সক্ষম ছিল। ব্যাবেজের কল্পনাপ্রসূত যন্ত্র বাস্তবায়নের জন্য প্রয়োজনীয় সঠিক প্রযুক্তি তার আমলে লভ্য ছিল না। রিলে, বায়ুশূন্য নল ও ট্রানজিস্টরের উদ্ভাবনের পরে বড় মাপের প্রোগ্রামযোগ্য গণনা সম্পাদন করা সম্ভবপর হয়। এই প্রযুক্তিগত উন্নতি গণিতের বেশ কিছু শাখায় বড় ধরনের সাহায্য করে, যেমন সাংখ্যিক বিশ্লেষণ ও সসীম গণিতের মতো ক্ষেত্রগুলিতে। এছাড়া এর ফলে গণিতের নতুন নতুন শাখারও উদ্ভব হয়, যেমন অ্যালগোরিদমসমূহের গবেষণা। সংখ্যাতত্ত্ব, ব্যবকলনীয় সমীকরণ ও বিমূর্ত বীজগণিতের মত বিচিত্র সব ক্ষেত্রে কম্পিউটার প্রযুক্তি একটি শক্তিশালী উপকরণ হিসেবে ব্যবহৃত হতে শুরু করে। এছাড়া কম্পিউটারের সুবাদে এমন সব গাণিতিক সমস্যা সমাধান খুঁজে পাওয়া সম্ভব হয়, যেগুলি অতীতে করা সম্ভব ছিল না। যেমন ১৯শ শতকের মধ্যভাগে প্রস্তাবিত চার বর্ণ টপোগাণিতিক সমস্যাটি সমাধান করা সম্ভব হয়। চার বর্ণ উপপাদ্যটিতে বলা হয় যে যেকোনও মানচিত্র অঙ্কনের জন্য চারটি বর্ণ বা রঙই যথেষ্ট, সাথে শর্ত হল দুইটি পাশাপাশি দেশের বর্ণ ভিন্ন হতে হবে। ১৯৭৬ সালে মার্কিন যুক্তরাষ্ট্রের ইলিনয় বিশ্ববিদ্যালয়ের একটি উচ্চ গণনক্ষমতাবিশিষ্ট কম্পিউটার ব্যবহার করে উপপাদ্যটি প্রমাণ করে দেখানো হয়।

আধুনিক বিশ্বে গণিতের ক্ষেত্রে জ্ঞান যে গতিতে অগ্রসর হয়েছে, তা অতীতে কখনও ঘটেনি। যেসমস্ত তত্ত্ব অতীতে একে অপর থেকে সম্পূর্ণ স্বতন্ত্র হিসেবে গণ্য করা হত, সেগুলিকে একীভূত করে সম্পূর্ণতর ও আরও বিমূর্ত তত্ত্ব গঠন করা হয়েছে। যদিও সবচেয়ে গুরুত্বপূর্ণ সমস্যাগুলির সিংহভাগই সমাধান করা হয়েছে, বেশ কিছু সমস্যা যেমন রিমানের অনুমিতিটি এখনও মীমাংসিত হয়নি। একই সময়ে নতুন নতুন উদ্দীপনামূলক সমস্যা আবির্ভূত হয়ে চলেছে। আপাতদৃষ্টিতে গণিতের সবচেয়ে বিমূর্ত তত্ত্বগুলিও বাস্তবে প্রয়োগ খুঁজে পাচ্ছে।

ভারতীয় সংখ্যার দশটি অঙ্ক, মানের উর্ধ্বক্রমে।

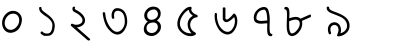
গণিতে অঙ্ক হলো সংখ্যা প্রকাশক চিহ্ন। কোনো সংখ্যায় একটি অঙ্কের দুধরনের মান থাকে, নিজস্ব মান ও স্থানীয় মান। দশমিক সংখ্যা পদ্ধতিতে ০ থেকে শুরু করে ৯ পর্যন্ত দশটি অঙ্ক আছে। এছাড়াও রয়েছে আরো নানা ধরনের সংখ্যা পদ্ধতি যেমনঃ বাইনারি( দুই ভিত্তিক সংখ্যা পদ্ধতি), অক্টাল ( আট ভিত্তিক), হেক্সাডেসিমাল ( ষোলো ভিত্তিক)। তবে দশমিক সংখ্যা পদ্ধতিই বিশ্বে সবচেয়ে জনপ্রিয় সংখ্যা পদ্ধতি ।

পরিমাণ বিষয়ক গবেষণার ভিত্তি হচ্ছে সংখ্যা। শুরুতেই আলোচিত হয় স্বাভাবিক সংখ্যা ও পূর্ণ সংখ্যা এবং এদের উপর সম্পন্ন বিভিন্ন গাণিতিক প্রক্রিয়া বা অপারেশন আলোচিত হয় পাটীগণিতে। পূর্নসংখ্যাগুলির গভীরতর ধর্মগুলি আলোচিত হয় সংখ্যাতত্ত্ব শাখায়। ফার্মার শেষ উপপাদ্য এই শাখার একটি বিখ্যাত ফলাফল। এখনও সমাধান হয়নি এরকম দুইটি সমস্যা হচ্ছে দ্বৈত মৌলিক সংখ্যা অনুমান এবং গোল্ডবাখের অনুমান।

আরও উন্নত সংখ্যাব্যবস্থায় পূর্ণসংখ্যাগুলি মূলদ সংখ্যার উপসেট হিসেবে পরিগণিত হয়। মূলদ সংখ্যাগুলি আবার বাস্তব সংখ্যার অন্তর্গত। বাস্তব সংখ্যাগুলি অবিচ্ছিন্ন রাশি বর্ণনা করতে ব্যবহার করা হয়। বাস্তব সংখ্যাগুলিকে আবার জটিল সংখ্যাতে সাধারণীকৃত করা হয়। জটিল সংখ্যাগুলিকে কোয়ার্টানায়ন ও অক্টোনায়োন-বিশিষ্ট সংখ্যাব্যবস্থায় সম্প্রসারিত করা যায়।

${\displaystyle 1,2,\ldots \,}$	${\displaystyle \ldots ,-1,0,1,\ldots \,}$	${\displaystyle {\frac {1}{2}},{\frac {2}{3}},0.125,\ldots \,}$	${\displaystyle \pi ,e,{\sqrt {2}},\ldots \,}$	${\displaystyle i,3i+2,e^{i\pi /3},\ldots \,}$
স্বাভাবিক সংখ্যা	পূর্ণ সংখ্যা	ভগ্নাংশ	বাস্তব সংখ্যা	জটিল সংখ্যা

সংখ্যা • হাইপারকমপ্লেক্স সংখ্যা • কোয়ার্টারনিয়ন • অক্টোনিয়ন • সেডেনিয়ন • হাইপাররিয়াল সংখ্যা • পরাবাস্তব সংখ্যা • পূরণবাচক সংখ্যা • অঙ্কবাচক সংখ্যা • পি-এডিক সংখ্যা • পূর্ণসাংখ্যিক অনুক্রম • গাণিতিক ধ্রুবক • সংখ্যার নাম • অসীম • ভিত্তি

আকার, প্রতিসাম্য এবং গাণিতিক গঠন সংক্রান্ত আলোচনা।

${\displaystyle 36\div 9=4}$		চিত্র:Rubik float.png

Monoids • Rings • ফীল্ড • রৈখিক বীজগণিত • বীজগাণিতিক জ্যামিতি • সার্বজনীন জ্যামিতি

স্থান নিয়ে গবেষণা মানব মনে গণিতের বীজ বপন করেছিল।

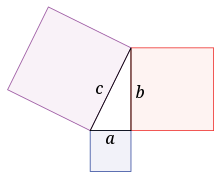
জ্যামিতি	ত্রিকোণমিতি	সমাকলন জ্যামিতি	টপোগণিত	ফ্র্যাক্টাল জ্যামিতি

বীজগাণিতিক জ্যামিতি • স্থানাংক পদ্ধতি • অন্তরক টপোগণিত • বীজগাণীতিক টপোগণিত • রৈখিক বীজগণিত • গুচ্ছবিন্যাসতাত্ত্বিক জ্যামিতি • বহুধা

গাণিতিক ফাংশন এবং সংখ্যার মানসমূহের পরিবর্তনের প্রকাশ।

		${\displaystyle {\frac {d^{2}}{dx^{2}}}y={\frac {d}{dx}}y+c}$
ক্যালকুলাস	ভেক্টর ক্যালকুলাস	ব্যবকলনীয় সমীকরণ	গতিশীল সিস্টেম	বিশৃঙ্খলা তত্ত্ব	জটিল-সাংখ্যিক বিশ্লেষণ

গাণিতিক বিশ্লেষণ • বাস্তব বিশ্লেষণ • জটিল বিশ্লেষণ • ফাংশনাল এনালিসিস • বিশেষ ফাংশন • পরিমাপন তত্ত্ব • ফুরিয়ার বিশ্লেষণ • পরিবর্তনশীল ক্যালকুলাস

গণিতের স্বভাব ও ধর্ম বুঝার জন্য সহায়ক।

${\displaystyle P\Rightarrow Q\,}$
গাণিতিক যুক্তি	সেট তত্ত্ব	ক্যাটাগরি তত্ত্ব

গণিতের ভিত্তি • গণিতের দর্শন • প্রাতিষ্ঠানিকতা • কনস্টাক্টিভিজম • প্রমাণ তত্ত্ব • মডেল তত্ত্ব • রিভার্স গণিত

বিচ্ছিন্ন গণিত

${\displaystyle {\begin{matrix}(1,2,3)&(1,3,2)\\(2,1,3)&(2,3,1)\\(3,1,2)&(3,2,1)\end{matrix}}}$
কম্বিনেটরিক্স	গণনার তত্ত্ব	ক্রিপ্টোগ্রাফি	লেখ তত্ত্ব

কম্পিউটিবিলিটি তত্ত্ব • কম্পিটেশনাল কমপ্লেক্স থিওরি • উপাত্ত তত্ত্ব

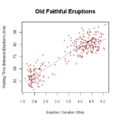
ফলিত গণিত গণিতের সাহায্যে বাস্তব-বিশ্বের বিভিন্ন সমস্যা সমাধান নির্দেশ করে।

• বলবিদ্যা • গাণিতিক অর্থনীতি • গাণিতিক জীববিজ্ঞান • ক্রিপটোগ্রাফি • অপারেশনস রিসার্চ

ফিল্ডস পদক হচ্ছে গণিতের সবচেয়ে মর্যাদাপূর্ণ পুরস্কার যেটি ১৯৩৬ সালে যাত্রা শুরু করে, বর্তমানে প্রতি চার বছর পরপর এই পুরস্কার দেওয়া হয । এই পুরষ্কারটিকে গণিতে নোবেল পুরষ্কারের সমতুল্য হিসেবে বিবেচনা করা হয়। তেইশটি উন্মুক্ত সমস্যার একটি বিখ্যাত তালিকা ১৯০০ সালে জার্মান গণিতবিদ ডাভিড হিলবের্ট তৈরি করেন যেটাকে বলা হয় "Hilbert's problems". এই তালিকাটি গণিতবিদদের মধ্যে অনেক বড় আলোড়ন তৈরি করে। এই সমস্যা গুলোর মধ্যে নয়টি সমস্যার সমাধান করা হয়েছে। সাতটি গুরুত্বর্পূণ সমস্যার একটি নতুন তালিকা "Millennium Prize Problems" নামে ২০০০ সালে প্রকাশিত হয়। এর প্রত্যেকটি সমস্যার সমাধানের জন্য এক মিলিওন ইউএস ডলার পুরস্কার ঘোষণা করা হয়।

দেখুন উপপাদ্যের তালিকা

পীথাগোরাসের উপপাদ্য • ফার্মির ভাগশেষ উপপাদ্য • গোডেলের অসম্পূর্ণতার তত্ত্ব • পাটীগণিতের মৌলিক উপপাদ্য • বীজণিতের মৌলিক উপপাদ্য • ক্যালকুলাসের মৌলিক উপপাদ্য • ক্যান্টরের কর্ণ-বৃদ্ধি • চার রঙ উপপাদ্য • যোরনের লেমা • অয়লারের অভেদ • গাউস-বনেট তত্ত্ব • কোয়াড্রাটিক রিসিপ্রোসিটি • রিম্যান-রখ তত্ত্ব।

বেশ কিছু গাণিতিক সমস্যা আছে, যা আজও সমাধান হয়নি।

গোল্ডবাখ অনুমান • দ্বৈত মৌলিক অনুমান • রিম্যান প্রকল্প • কোলাজ অনুমান • P=NP? • open হিলবার্টের সমস্যাগুচ্ছ।