மரபார்ந்த விசையியல்
மரபார்ந்த விசையியல், எறிபொருட்கள், இயந்திர உறுப்புக்கள் போன்றனவும்; விண்கலங்கள், கோள்கள், விண்மீன்கள், விண்மீன் கூட்டங்கள் போன்ற வானியல் பொருட்கள் போன்றனவுமான கண்ணுக்குத் தெரியக்கூடிய பொருட்களின் இயக்கங்களை விளக்குவதற்குப் பயன்படும் ஒரு துறை. மேற்குறிப்பிட்ட பெரிய பொருட்களின் இயக்கங்கள் தொடர்பில் துல்லியமான முடிவுகளை வழங்கக்கூடிய மரபார்ந்த விசையியல் துறை; அறிவியல், பொறியியல், தொழில்நுட்பம் ஆகிய துறைகளில் மிகப் பழையதும், மிகப் பெரியதுமான ஒரு பகுதியும் ஆகும்.
| மரபார்ந்த விசையியல் | ||||||||
வரலாறு · காலக்கோடு
| ||||||||
இவை தவிர இதில், வளிமங்கள், நீர்மங்கள், திண்மங்கள் ஆகியவை தொடர்பிலான சிறப்புப் பகுதிகளும் உண்டு. இயற்பியலில், பொருட்களினதும், பொருட் தொகுதிகளினதும் இயக்கங்களைக் கட்டுப்படுத்துவனவும், கணிதவியல் அடிப்படையில் விளக்குவனவுமான இயற்பியல் விதிகளோடு தொடர்புள்ள, விசையியல் தொடர்பான இரண்டு துணைப் பிரிவுகளில் மரபார்ந்த விசையியல் ஒன்றாகும். மற்றது குவாண்டம் விசையியல். இது நியூட்டோனியன் விசையியல் என்றும் அறியப்படுகிறது.[1][2][3] இருப்பினும் நூலாசிரியர்கள் பெரும்பாலும் நியூட்டோனியன் விசையியலை, லெக்ராஞ்சியன் விசையியல் மற்றும் ஆமில்டோனியன் விசையியலுடன் ஒன்றாக, மரபார்ந்த விசையியலின் முறைப்படுத்தல்களாகக் காண்கின்றனர்.

குறிப்பிடத்தக்களவுக்குப் பெரிய (நாம் அன்றாட வாழ்வில் பயன்படுத்தும் பொருட்கள்), வெற்றிடத்தில் ஒளியின் வேகத்தொடு (c=3.0*10^8) ஒப்பிட்டால் மிகவும் குறைந்த வேகமுடைய பொருட்களோடு சம்பத்தப்பட்ட கணிப்புகளிலேயே மரபார்ந்த விசையியலைப் பயன்படுத்த முடியும். சாதாரண வாகனங்கள் பயணிப்பது, விண்கலங்கள், பந்து, ஆணி இவ்வாறான பொருட்களோடு சம்பத்தப்பட்ட கணிப்புகளில் மரபார்ந்த விசையியல் மிகத்துல்லியமான விளைவைத் தருகின்றது. எனினும் அணுக்கள், உப-அணுத் துணிக்கைகள் சம்பந்தமான கணிப்புகளில் குவாண்டம் விசையியலைப் பயன்படுத்தினால் மாத்திரமே வழு வீதம் குறைவான விளைவை எதிர்பார்க்கலாம். வேகம் ஒளியின் வேகத்தை அண்மிக்கும் சந்தர்ப்பத்திலும் மரபார்ந்த விசையியலைப் பயன்படுத்த இயலாது. மிகச்சிறிய துணிக்கைகள் ஒளியின் வேகத்தை அண்மிக்கும் சந்தர்ப்பங்களில் குவாண்டம் புலக்கோட்பாடைப் பயன்படுத்துவதே சிறப்பானதாகும்.
மரபார்ந்த விசையியல் என்ற தொடரானது 20 ஆம் நூற்றாண்டின் ஆரம்பத்தில் வரையறுக்கப்பட்டது. அது 17 ஆம் நூற்றாண்டில் அக்காலத்திய இயற்கை கருத்தியலாளர்கள் பலர் மற்றும் ஐசாக்கு நியூட்டனால் தொடங்கப்பட்ட இயற்பியலின் அமைப்பை விவரிக்கிறது. இத்துறை ஜோஹென்னாசு கெப்ளரின் ஆரம்பகால வானியல் கருத்தியல்கள் கட்டமைக்கப்பட்டுள்ளது, மேலும் டைகோ பிராகேவின் துல்லிய உற்றுநோக்கல்கள் மற்றும் கலிலியோவின் இடமார்ந்த எறிபொருள் இயக்க ஆய்வுகளை அடிப்படையாகவும் கொண்டுள்ளது. இயற்பியலின் இந்த அம்சங்கள் குவாண்டம் இயற்பியல் மற்றும் சார்பியலின் தோற்றத்திற்கு வெகுகாலத்திற்கு முன் உருவாக்கப்பட்டதால், அவற்றின் சில மூலங்கள் ஐன்சுடைனின் சார்பியல் கொள்கையை இவ்வகையிலிருந்து விலக்குகின்றன. இருப்பினும் நவீன மூலங்கள், சார்பியல் விசையியலையும், அவர்களின் பார்வையில் நன்கு வளர்ச்சியடைந்த மற்றும் துல்லியமான மரபார்ந்த விசையியல் வடிவமாகச் சேர்க்கின்றன.
ஆரம்பகால மரபார்ந்த விசையியில் பெரும்பாலும் நியூட்டன் விசையியல் என்று குறிக்கப்படுகிறது. அது கணித முறையின் மூலம் நியூட்டன், இலிப்பினிட்சு போன்றவர்களால் விவரிக்கப்பட்ட இயற்பியல் கருத்தாக்கங்களைக் கொண்டுள்ளது. பிற்காலத்தில் மிக சுருக்கமான மற்றும் பொதுவான முறைகள் உருவாக்கப்பட்டன, இவை மரபார்ந்த விசையியலை, லெக்ராஞ்சியின் விசையியல் மற்றும் ஆமில்டோனியன் விசையியல் என மறு வரையறை இட்டுச் சென்றன. இந்த மேம்பாடுகள், 18 மற்றும் 19 வது நூற்றூண்டில் பெரும்பாலும் உருவாக்கப்பட்டன, அவை நியூட்டனின் பணிகளுக்கு மேலாக, குறிப்பாக அவற்றின் பகுப்பிய விசையியலின் பயன்பாட்டின் மூலம் விரிவாக எடுத்துச் சென்றன.
கோட்பாட்டு விளக்கங்கள்
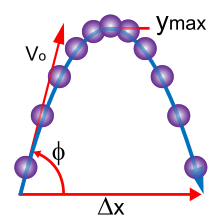
பின்வருவன மரபார்ந்த விசையியலின் அடிப்படை கருத்துகளை அறிமுகப்படுத்துகின்றன. மரபார்ந்த விசையியலில் கணித்தலை இலகுவாக்குவதற்காக பொருட்களை தனிப் புள்ளிகளாகக் (தவிர்க்கக்கூடிய அளவினைக் கொண்ட பொருட்கள்) கருத வேண்டும். மரபார்ந்த விசையியலில் அப்புள்ளிப் பொருள் உள்ள இடம், அதன் திணிவு மற்றும் அதில் தாக்கும் விசைகள் மாத்திரமே கருத்தில் கொள்ளப்படும்.
உண்மையில் எந்தவொரு பொருளும் புள்ளிப் பொருளாகத் தொழிற்பட முடியாது. மரபார்ந்த விசையியல் வரையறுக்கும் பொருட்கள் அனைத்தும் சுழியமற்ற அளவினையே கொண்டுள்ளன. (மிகச் சிறிய பொருட்களான இலத்திரன் போன்றவற்றின் இயற்பியல், குவாண்டம் விசையியலால் துல்லியமாக விவரிக்கப்படுகிறது) சுழியமற்ற அளவினைக் கொண்ட பொருட்கள், அவற்றின் கூடுதல் கட்டின்மையளவுகள் காரணமாக கற்பனையான தனிப்புள்ளிகளை விட சிக்கலான நடத்தையினைக் கொண்டுள்ளன. எகா. ஒரு அடிபந்தால் அது நகரும்போதே சுழலவும் முடியும். இருப்பினும், புள்ளி பொருட்கள்களைப் பயன்படுத்தி அத்தகைய பொருட்களை பல புள்ளிப் பொருட்கள் கூட்டாக செயல்படுவதால் உருவாக்கப்பட்ட கூட்டு பொருட்களாகக் கருதுவதின் மூலம் படிக்க முடியும் மரபார்ந்த விசையியலில் ஒரு பொருளின் திணிவு மையமே புள்ளிப் பொருளாகக் கருதப்படும். உதாரணமாக 1 kg பந்தைக் கருதினால் கணித்தலின் போது அப்பந்தின் மையப் பிரதேசத்துக்கே 1 kg திணிவு வழங்கப்பட்டு, அனைத்து விசைகளும் அம்மையப் புள்ளியில் தொழிற்படுவதாகவே கருதப்படும்.
மரபார்ந்த விசையில் பருப்பொருள் மற்றும் விசைகள் எப்படி உள்ளன மற்றும் எவ்வாறு செயலாற்றுகின்றன என்பதின் பொதுவான குறியீடுகளைப் பயன்படுத்துகிறது. அது பருப்பொருள் மற்றும் ஆற்றல் ஆகியன வரையறுக்கப்பட்ட, அறிந்த பண்புகளான வெளியின் அமைவிடம் மற்றும் வேகம் போன்றவற்றைக் கொண்டுள்ளது என்று கருதுகிறது. சார்பியலற்ற விசையியலும் விசைகள் உடனடியாக செயல்படுவதாகக் கருதுகிறது.
பொருள் இயங்கும் இடம் (நிலை மற்றும் அதன் வகைக்கெழுக்கள்)
| நிலை | m |
| கோண நிலை/கோணம் | அலகில்லை (ரேடியன்) |
| திசைவேகம் | m·s−1 |
| கோணத் திசைவேகம் | s−1 |
| ஆர்முடுகல் | m·s−2 |
| கோண ஆர்முடுகல் | s−2 |
| jerk | m·s−3 |
| "கோண திடுக்கம்" | s−3 |
| அலகு ஆற்றல் | m2·s−2 |
| உட்கொள்ளப்பட்ட அளவு வீதம் | m2·s−3 |
| நிலைமத் திருப்புத்திறன் | kg·m2 |
| உந்தம் | kg·m·s−1 |
| கோண உந்தம் | kg·m2·s−1 |
| விசை | kg·m·s−2 |
| திருப்பு விசை | kg·m2·s−2 |
| ஆற்றல் | kg·m2·s−2 |
| திறன் | kg·m2·s−3 |
| அழுத்தம் மற்றும் ஆற்றல் அடர்த்தி | kg·m−1·s−2 |
| பரப்பு இழுவிசை | kg·s−2 |
| சுருள் மாறிலி | kg·s−2 |
| கதிர்வீச்சு மற்றும் ஆற்றல் பாயம் | kg·s−3 |
| இயக்க பாகியல் | m2·s−1 |
| மாறும் பாகியல் | kg·m−1·s−1 |
| அடர்த்தி (நிறை அடர்த்தி) | kg·m−3 |
| அடர்த்தி (எடை அடர்த்தி) | kg·m−2·s−2 |
| எண் அடர்த்தி | m−3 |
| வினை | kg·m2·s−1 |
ஒரு புள்ளிப்பொருளின் நிலையானது வெளியில் ஆள்கூற்று முறைமை உதவியால் குத்துமதிப்பாக குறிக்கப்பட்ட புள்ளி O படி வரையறுக்கப்படுகிறது. ஒரு எளிய ஆட்கூறு முறைமை ஒரு துகள் Pயை, மூலம் Oவிலிருந்து புள்ளி Pயை நோக்கிய r என்று அடையாளமிடப்பட்ட ஒரு திசையனால் வரையறுக்கலாம். பொதுவாக புள்ளிப் பொருள் Oவைப் பொருத்து நிலையாக இருக்க வேண்டியதில்லை. Oவைப் பொருத்து P நகரும் நிகழ்வுகளில், r ஆனது நேரம் tஇன் சார்பின் வகைக்கெழுவாக வரையறுக்கப்படுகிறது. ஐன்சுடைனுக்கு முந்தைய சார்பியலில் (கலிலியோ சார்பியலில்) நேரமானது சார்பற்றதாகக் கருதப்படுகிறது, அ.து இரு கொடுக்கப்பட்ட நிகழ்வுகளுக்கு இடையே உற்றுநோக்கப்படும் நேரமானது அனைத்து உற்றுநோக்காளர்களுக்கும் சமமாகும்.[4] சார்பற்ற நேரத்தைச் சார்ந்திருப்பதுடன், மரபார்ந்த விசையியல் வெளியின் கட்டமைப்பாக யூக்ளிடின் வடிவியலைக் கருதுகிறது.[5] வேகம், கதி,ஆர்முடுகல் என்பன பொருள் இயங்கும் இடம்/ நிலையுடன் தொடர்புபட்ட கணியங்களாகும்.
திசைவேகம் மற்றும் வேகம்
ஒரு அலகு நேரத்தைல் ஏற்பட்ட இடப்பெயர்ச்சி வேறுபாடே வேகம் ஆகும்.
- .
இதன் போது பொருள் இயங்கும் திசையையும் குறிப்பது அவசியமாகும். நேர்கோட்டு இயக்கத்தின் போது இரு இயங்கும் பொருட்களைக் கருதும் போது திசைக்கேற்றபடி வேகத்தை ஒன்றோடொன்று கூட்டவோ கழிக்கவோ முடியும். உதாரணமாக ஒரு கார் 50 km/h வேகத்துடன் செல்கின்றது. அக்காரை 60 km/h இல் செல்லும் கார் முந்திக் கொண்டு செல்கின்றது. இவற்றின் புவி சார்பான வேகம் இவ்வாறு காணப்பட்டாலும், மெதுவாகச் செல்லும் காரில் உள்ளவர் முந்திக் கொண்டு செல்லும் கார் 60-50= 10 km/h வேகத்தில் செல்வதாகவும், வேகமாகச் செல்லும் காரில் உள்ளவர் மற்றைய கார் பின்னோக்கி 10 km/h அல்லது -10 km/h செல்வதாகவே எண்ணுவார். இது சார்பு வேகம் எனப்படும். இதே போன்று எதிர்த்திசையில் கார்கள் சென்றிருந்தால் வேகங்களைக் கூட்ட வேண்டும்.
ஆர்முடுகல்
ஒரு அலகு நேரத்தில் ஏற்பட்ட வேக மாற்றமே/ திசைவேக மாற்றமே ஆர்முடுகலாகும். வேகம் கூடுவதோ, குறைதலோ, வேகத்தின் திசை மாற்றமடைதலோ ஆர்முடுகலைத் தோற்றுவிக்கும்.
வேகம் குறைவடைந்து கொண்டு செல்லல் அமர்முடுகல் என பொதுவாக அழைக்கப்பட்டாலும், அதுவும் விசையியலில் ஆர்முடுகலின் ஒரு வகையாகவே கருதப்படும்.
விசை மற்றும் உந்தம்
விசையானது உந்தத்துக்கு நேர்விகிதமானது. இத்தொடர்பை நியூட்டன் என்ற விஞ்ஞானியே முதலில் கண்டுபிடித்தார். இது நியூட்டனின் இரண்டாம் விதி எனவும் அழைக்கப்படுகின்றது.
மேற்கூறிய சமன்பாட்டில் mv (திணிவு*வேகம்) என்பது உந்தத்தைக் குறிக்கிறது. எனவே இச்சமன்பாடு படி ஒரு அலகு நேரத்தில் ஏற்பட்ட உந்த மாற்றமே விசையாகும். ஆர்முடுகலுக்கான சமன்பாடு a = dv/dt என்பதால், மேற்படிச் சமன்பாட்டை பின்வருமாறு காட்டலாம்.
எனவே ஒரு பொருளில் சமப்படுத்தப்படாத புறவிசை (F) தொழிற்படும் போது அப்பொருளுக்கு ஆர்முடுகல் (a) காணப்படும். பொருளின் திணிவு (m) அதிகரிக்க ஆர்முடுகல் குறைவடையும்.
ஒரு பொருளில் செயற்படுத்தப்படும் விசை தெரியும் வரையில், அப்பொருளின் இயக்கத்தை விவரிக்க நியூட்டனின் இரண்டாம் விதி போதுமானது. ஒரு புள்ளியில் செயல்படும் ஒவ்வொரு விசையின் சார்பற்ற தொடர்புகள் கிடைக்கும் போது, அவற்றை நியூட்டனின் இரண்டாம் விதியில் பிரதியிட்டு ஒரு சாதாரண வகைக்கெழு சமன்பாட்டைப் பெறலாம். இந்த வகைக் கெழு சமன்பாடு, இயக்கத்தின் சமன்பாடு எனப்படுகிறது.
வேலை மற்றும் சக்தி
ஒரு பொருளின் மீது மாறா விசை F ஆனது தொழிற்பட்டு பொருளை Δr தூரம் நகர்த்தினால் இங்கு இவ்விசையால் அப்பொருள் மீது வேலை செய்யப்படுகின்றது. எனவே விசையியலில் வேலையானது விசை மற்றும் தூரம் ஆகிய கணியங்களின் பெருக்கமாக உள்ளது.
m திணிவுடைய பொருள் v வேகத்துடன் இயங்குமாயின் அதன் இயக்க சக்தி Ek ஆனது பின்வருமாறு வரையறுக்கப்படுகின்றது.
மேற்கோள்கள்
- Bettini, Alessandro (2016). A Course in Classical Physics 1—Mechanics. Springer. பக். vii. பன்னாட்டுத் தரப்புத்தக எண்:978-3-319-29256-4.
- French, A.P. (1971). Newtonian Mechanics. New York: W. W. Norton & Company. பக். 3. பன்னாட்டுத் தரப்புத்தக எண்:0-393-09970-9.
- Kleppner, Daniel; Kolenkow, Robert (2014). An Introduction to Mechanics (Second ). Cambridge: Cambridge University Press. பக். 49. பன்னாட்டுத் தரப்புத்தக எண்:978-0-521-19811-0.
- Knudsen, Jens M.; Hjorth, Poul (2012). Elements of Newtonian Mechanics (illustrated ). Springer Science & Business Media. பக். 30. பன்னாட்டுத் தரப்புத்தக எண்:978-3-642-97599-8. https://books.google.com/books?id=rkP1CAAAQBAJ. Extract of page 30
- MIT physics 8.01 lecture notes (page 12) (PDF)
