تصادفی متغیر
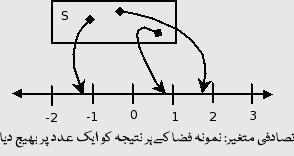
تصادفی متغیر اپنے نام کے باوجود نہ تو حادثاتی (یا اتفاقی) ہوتا ہے اور نہ ہی متغیر۔ بلکہ یہ ایک دالہ ہے جس کا ساحہ نمونہ فضا اور حیطہ اعداد ہوتے ہیں۔ جیسا کہ تصویر 1 میں دکھایا گیا ہے، نمونہ فضا S کے ہر نتیجہ کے ساتھ ایک عدد مخصوص کر دیا گیا ہے۔ دالہ کی تعریف کے مطابق ایک سے زیادہ "نتائج" کے لیے ایک ہی عدد مخصوص کرنا ممکن ہے، البتہ ایک نتیجہ کے لیے ایک سے زیادہ عدد مخصوص کرنے کی اجازت نہیں۔
| اصطلاح | term |
|---|---|
|
تصادفی متغیر |
random variable |
نمونہ فضا پر تصادفی متغیر تعریف کر کے واقعات کو تصادفی متغیر کے استعمال سے بیان کیا جا سکتا ہے۔ تصادفی متغیر کی بدولت گوناں گوں نمونہ فضاؤں کی خصوصیات ریاضی کی یکساں زبان میں بیان کی جا سکتی ہیں، مسائل کے حل کے لیے ریاضی آلات تیار کیے جا سکتے ہیں اور مسلئہ اثباتی ڈھونڈے جا سکتے ہیں۔
متفرد تصادفی متغیر
ایسے تصادفی متغیر کو متفرد کہا جاتا ہے، اگر اس کی تمام ممکنہ اقدار متفرد مجموعہ ہوں۔
مثال
دو چھ اطرافی طاس، سبز اور سرخ رنگ کے، کو اچھالا جاتا ہے۔
- تصادفی متغیر S سبز اور سرخ طاس کے اعداد کی جمع ہے۔ اس کا حیطہ ہو گا۔
- تصادفی متغیر D سبز اور سرخ طاس کے اعداد کا فرق ہے۔ اس کا حیطہ ہو گا۔
- تصادفی متغیر M سبز اور سرخ طاس کے اعداد کا اکبر ہے۔ اس کا حیطہ ہو گا۔
یہ تینوں تصادفی متغیر متفرد ہیں۔
توزیع احتمال
تفصیلی مضمون: توزیع احتمال
متفرد تصافی متغیر X کی احتمال کمیت دالہ کسی بھی عدد x کے لیے یوں تعریف ہوتی ہے
یعنی اس احتمال کے برابر ہے کہ تصادفی متغیر X کی قدر x بنے۔ یہاں S نمونہ فضا ہے، جو تصادفی متغیر X کا ساحہ ہے۔ غور کرو کہ
اب متفرد تصادفی متغیر X کی تَراكُمی توزیع احتمال دالہ یوں تعریف ہو گی
یعنی یہ احتمال کہ تصادفی متغیر X کی قدر x کے برابر یا اس سے کم ہو۔ غور کرو کہ
متفرد تصادفی متغیر X کے لیے اس کے "احتمال کمیت دالہ" اور "تَراكُمی توزیع احتمال دالہ" ، دونوں کو "توزیعِ احتمال" پکارا جاتا ہے۔
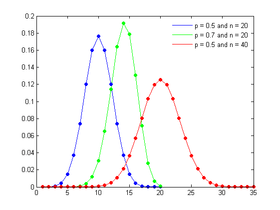
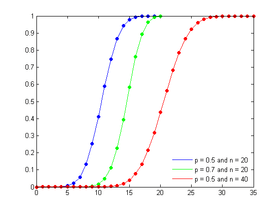
مثال: دو رقمی توزیعِ احتمال
تفصیلی مضمون: دو رقمی توزیع احتمال
بعض اوقات ایک ہی تجربہ کو متعدد بار دہرایا جاتا ہے (جیسے سکے کو بار بار فضا میں اچھالا جائے)۔ ایسے بار بار آزمائش میں فرض کرو کہ:
- دو ممکنہ نتائج ہیں، "کامیابی" اور "ناکامی"
- ہر آزمائش پر "کامیابی" کا احتمال p ہے اور "ناکامی" کا احتمال
- آزمائش کی تعداد n ہے
- ہر آزمائش دوسری آزمائشوں سے آزاد ہے
فرض کرو کہ تصادفی متغیر X ہے، جو ان n آزمائشوں میں "کامیابی" کی تعداد ظاہر کرتا ہے۔ اس متفرد تصادفی متغیر کا حیطہ
ہے اور توزیعِ احتمال
اس توزیع احتمال کو "دو رقمی توزیع" کے نام سے پکارا جاتا ہے۔ ( یہاں ! کی علامت عامِلیہ کو ظاہر کرتی ہے۔)
متوقع قدر
تفصیلی مضمون: متوقع قدر
تصادفی متغیر X کی متوقع قدر اس کی احتمال کمیت دالہ سے وزن شدہ اوسط کو کہتے ہیں اور اس متوقع قدر کو یوں تعریف کیا جاتا ہے
متوقع قدر کو تصافی متغیر X کی احتمال کمیت دالہ کا مرکزِ کشش ثقل سمجھا جا سکتا ہے۔
مثال: دو رقمی توزیعِ احتمال شدہ تصادفی متغیر X کی متوقع قدر
تصویر 2 میں سرخ خطِ منحنی کے مطابق
متوقع قدر کو تصادفی متغیر کا اوسط بھی کہا جاتا ہے۔
تفاوت
تفصیلی مضمون: تفاوت
تصادفی متغیر کا اپنی متوقع قدر سے ممکنہ انحراف کی مقدار کو جانچنے کے لیے، تصادفی متغیر کا تَفاوُت استعمال ہوتا ہے۔ اگر تصادفی متغیر X کی متوقع قدر کو
لکھا جائے، تو X کا تَفاوُت (variance) یوں تعریف کیا جاتا ہے
جہاں غور کرو کہ متغیر کی وزن شدہ اوسط ہے، جہاں وزن تصادفی متغیر X کی احتمال کمیت دالہ سے کیا گیا ہے۔
اس تَفاوُت کے مربع جزر کو تصادفی متغیر کا معیاری انحراف کہا جاتا ہے، جو یہ بتاتا ہے کہ تصادفی متغیر کی ممکنہ اقدار کا اپنی متوقع قدر کے گرد پھیلاؤ کتنا سمجھا جا سکتا ہے۔ معیاری انحراف (standard deviation)
مثال: دو رقمی توزیعِ احتمال شدہ تصادفی متغیر X کا
تصویر 2 میں سرخ خطِ منحنی کے مطابق تَفاوُت اور معیاری انحراف
تصادفی متغیر کا دالہ
دی گئی دالہ ، تو کسی تصادفی متغیر X کے لیے،
بھی ایک تصادفی متغیر ہو گا اور اس کی تَراكُمی توزیع احتمال یوں لکھی جا سکتی ہے، تصادفی متغیر X کی تَراكُمی توزیع احتمال کے استعمال سے :