சமவிசைசார் புள்ளி
யூக்ளிடிய வடிவவியலில் ஒரு முக்கோணத்தை எந்தவொரு புள்ளியை மையமாகக் கொண்டு நேர்மாற்றும்போது அம்முக்கோணமானது சமபக்க முக்கோணமாக உருமாற்றமடைகிறதோ, அந்தப் புள்ளியே அம்முக்கோணத்தின் சமவிசைசார் புள்ளி (isodynamic point) எனப்படும். மேலும் முக்கோணத்தின் ஒவ்வொரு உச்சிக்கும் சமவிசைசார் புள்ளிக்கும் இடைப்பட்ட தூரமானது அந்தந்த உச்சிக்கு எதிரிலமையும் முக்கோணப் பக்கநீளங்களுக்கு எதிர்விகிதத்தில் இருக்கும். சமபக்க முக்கோணத்திற்கு அதன் நடுக்கோட்டுச்சந்தி மட்டுமே ஒரேயொரு சமவிசைசார் புள்ளியாக அமையும்ம். ஒவ்வொரு அசமபக்க முக்கோணத்திற்கும் இரு சமவிசைசார் புள்ளிகள் உள்ளன. கணிதவியலாளர் ஜோசப் நியுபெர்க் இப்புள்ளிகள் பற்றி ஆய்வு செய்து அவற்றுக்கு இப்பெயரிட்டார்[1].
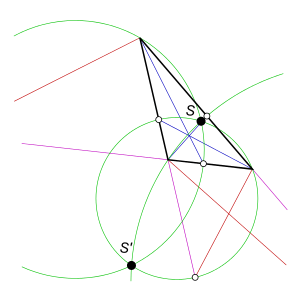
சமவிசைசார் புள்ளிகள் இரண்டும் முக்கோண மையங்களாகும். மேலும் இவை மோபியஸ் உருமாற்றங்களின் கீழும் மாறாநிலை கொண்டவையாக இருக்கும்.
தொலைவு விகிதங்கள்
முக்கோணத்தின் சமவிசைசார் புள்ளிகள் , எனில், கீழ்க்காணும் சமன்பாடுகள் உண்மையாய் இருக்கும்:
அதாவது தொலைவுகள் , , மூன்றும் முக்கோணத்தின் பக்க நீளங்கள் , , மூன்றுக்கும் எதிர்விகிதத்தில் இருக்கும்.
முக்கோணத்தின் அப்பலோனியஸ் வட்டங்கள் மூன்றும் வெட்டிக்கொள்ளும் பொதுப்புள்ளிகளாக , இரண்டும் உள்ளன. இவ் வட்டங்கள் ஒவ்வொன்றும் முக்கோணத்தின் ஒரு உச்சி வழிச் செல்வதாகவும், மற்ற இரு உச்சிகளிலிருந்து மாறாத் தொலைவு விகிதம் கொண்டதாகவும் இருக்கின்றன.[3] எனவே ஒவ்வொரு சோடி அப்பலோனியஸ் வட்டங்களின் சமதொடுகோட்டு அச்சாக அமைகிறது. கோட்டுத்துண்டு இன் நடுக்குத்துக்கோடானது அப்பலோனியஸ் வட்டமையங்கள் அமைகின்ற லெமாய்ன் கோடாகும்.[4]
உருமாற்றங்கள்
ஒரு புள்ளி நேர்மாற்றம் மற்றும் மோபியஸ் உருமாற்றங்களைப் பொறுத்து அமையும் பண்புகளைக் கொண்டும் முக்கோணத்தின் சமவிசைசார் புள்ளிகள் and இரண்டையும் வரையறுக்கலாம்.
சமவிசைசார் புள்ளியைப் பொறுத்த நேர்மாற்றத்தால் முக்கோணம் ஆனது ஒரு சமபக்க முக்கோணமாக மாறுகிறது.[5] சுற்றுவட்டத்தைப் பொறுத்த நேர்மாற்றத்தால் மாற்றமடைவதில்லை; எனினும் இவ்வுருமாற்றத்தில் அதன் ஒரு சமவிசைசார் புள்ளி மற்றொரு விசைசார் புள்ளியாக மாறுகிறது.[3]
முக்கோணம் இன் சுற்றுவட்டத்தின் உட்புறத்தை இன் உருமாற்ற முக்கோணத்தின் சுற்றுவட்டத்தின் உட்புறமாகவே உருமாற்றும் மோபியஸ் உருமாற்றங்களினால் சமவிசைசார் புள்ளிகள் நிலைமாறாமல் உள்ளன. ஆனால் சுற்றுவட்டத்தினை உள்ளும் வெளியுமாக மாற்றும் உருமாற்றங்களில் சமவிசைசார் புள்ளிகள் ஒன்று மற்றதாக மாற்றப்படுகின்றது.[6]
கோணங்கள்
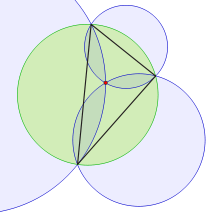
அப்பலோனியஸ் வட்டங்களின் வெட்டும் புள்ளிகளாக அமைகின்ற சமவிசைசார் புள்ளிகளை வேறு மூன்று வட்டங்களின் வெட்டும் புள்ளிகளாக அமைவதையும் காணலாம்:
முக்கோணத்தின் உச்சிகளாலான , , ஆகிய மூன்று சோடிப் புள்ளிகளின் வழியாகக் செல்வதும், முக்கோணத்தின் சுற்றுவட்டத்தினை 2π/3 அளவு உச்சிக்கோணம் கொண்ட வில்லையில் வெட்டுவதுமான மூன்று வட்டங்களும் முக்கோணம் இன் முதல் சமவிசைசார் புள்ளியில் வெட்டிக் கொள்கின்றன.
இதேபோல, , , வழியாகக் செல்வதும், முக்கோணத்தின் சுற்றுவட்டத்தினை π/3 அளவு உச்சிக்கோணம் கொண்ட வில்லையில் வெட்டுவதுமான மூன்று வட்டங்களும் முக்கோணம் இன் இரண்டாவது சமவிசைசார் புள்ளியில் வெட்டிக் கொள்கின்றன.[6]
முக்கோணத்தின் மூன்று உச்சிகளோடும் சமவிசைசார் புள்ளிகள் உருவாக்கும் கோணங்கள் பின்வரும் சமன்பாடுகளை நிறைவு செய்கின்றன[6]:
முக்கோணத்தின் மூன்று பக்கங்களிலும் சமவிசைசார் புள்ளி ஐ எதிரொளிப்பதால் கிடைக்கும் புள்ளிகளாலான முக்கோணம் ஒரு சமபக்க முக்கோணம் ஆகும். அதைப் போலவே, இலிருந்து முக்கோணத்தின் மூன்று பக்கங்களுக்கும் வரையப்படும் செங்குத்துக்கோடுகளின் அடிப்புள்ளிகளால் உருவாகும் பாத முக்கோணமும் சமபக்க முக்கோணமாக இருக்கும்.[5][7] முக்கோணத்தினுள் வரையப்படும் சமபக்க முக்கோணங்களில் மிகக் குறைந்த பரப்பளவு கொண்டது பாத முக்கோணம் ஆகும்.[8]
வரையும் முறை
அப்பலோனியஸ் வட்டங்களின் வெட்டும்புள்ளிகளாக
- முக்கோணத்தின் உச்சிக்கோணம் இன் உட்கோண மற்றும் வெளிக்கோண இருசமவெட்டிகள் வரைந்து கொள்ள வேண்டும்
- இக்கோண இருசமவெட்டிகள் இரண்டும் முக்கோணத்தின் பக்கம் ஐ வெட்டும் இரு புள்ளிகள் காண வேண்டும்.
- இவ்விரு புள்ளிகளையும் இணைக்கும் கோட்டுத்துண்டை விட்டமாகக் கொண்ட வட்டம் வரைய வேண்டும்.
- இவ்வட்டமே முக்கோணத்தின் உச்சி இன் வழிச் செல்லும் அப்பலோனியஸ் வட்டம் ஆகும்.
- இவ்வாறு மற்றொரு உச்சி வழியாகச் செல்லும் இரண்டாவது அப்பலோயஸ் வட்டம் வரைய வேண்டும்.
- இவ்விரு வட்டங்களும் வெட்டிக்கொள்ளும் இருபுள்ளிகளே முக்கோணத்தின் சமவிசைசார் புள்ளிகளாகும். [3]
முக்கோணத்தின் எதிரொளிப்பையும் உட்புற-வெளிப்புறமான சமபக்க முக்கோணம் மூலமாக
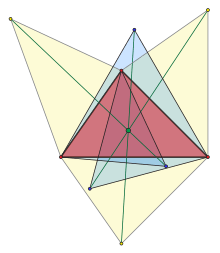
- முக்கோணத்தின் பக்கம் இல் உச்சி இன் எதிரொளிப்பு காண வேண்டும். ( , ஐ மையங்களாகக் கொண்டு ) வழியே செல்லும் வட்டங்கள் வெட்டும் புள்ளி)
- ஐ ஒரு பக்கமாகக் கொண்டு உட்புறமாக ஒரு சமபக்க முக்கோணம் வரையப்படுகிறது.
- இம்முக்கோணத்தின் உச்சி
- இதேபோல முக்கோணத்தின் மற்ற இரு உச்சிகளுக்கும் புள்ளிகள் காணப்படுகின்றன.
- , , கோடுகள் மூன்றும் முதல் சமவிசைசார் புள்ளியின் சந்திக்கின்றன.
- இரண்டாவது சமவிசைசார் புள்ளிகள் சமபக்க முக்கோணத்தை வெளிப்புறமாக வரைவதன் மூலம் இரண்டாவது சமவிசைசார் புள்ளி காணப்படுகிறது.[9]
முந்நேரியல் ஆயதொலைவுகள் மூலமாக
சமவிசைசார் புள்ளிகளின் முந்நேரியல் ஆயதொலைவுகள் மூலமாக அவற்றைக் காணலாம்[10]
- முதல் சமவிசைசார் புள்ளியின் முந்நேரியல் ஆயதொலைவுகள்:
- இதன் மூலமாக முதல் சமவிசைசார் புள்ளியின் இருப்பிடத்தையும்;
- இரண்டாவது சமவிசைசார் புள்ளியின் முந்நேரியல் ஆயதொலைவுகள்:
- மூலமாக இரண்டாவது சமவிசைசார் புள்ளியின் இருப்பிடத்தையும் காணலாம்.
குறிப்புகள்
- For the credit to Neuberg, see e.g. Casey (1893) and Eves (1995).
- Neuberg (1885) states that this property is the reason for calling these points "isodynamic".
- Bottema (2008); Johnson (1917).
- Wildberger (2008).
- Casey (1893); Johnson (1917).
- Rigby (1988).
- Carver (1956).
- Moon (2010).
- Evans (2002).
- Kimberling (1993).
மேற்கோள்கள்
- Bottema, Oene (2008), Topics in elementary geometry (2nd ), Springer, p. 108, பன்னாட்டுத் தரப்புத்தக எண்:9780387781303, http://books.google.com/books?id=oznMpzdFsWYC&pg=PA108.
- Carver, Walter B. (1956), "Some geometry of the triangle", American Mathematical Monthly 63 (9): 32–50.
- Casey, John (1893), A treatise on the analytical geometry of the point, line, circle, and conic sections: containing an account of its most recent extensions, with numerous examples, Dublin University Press series, Hodges, Figgis, & Co., p. 303, http://books.google.com/books?id=Ah5IAAAAIAAJ&pg=PA303.
- Evans, Lawrence S. (2002), "A rapid construction of some triangle centers", Forum Geometricorum 2: 67–70, http://forumgeom.fau.edu/FG2001volume1/FG200109.pdf.
- Howard Eves (1995), College geometry, Jones & Bartlett Learning, pp. 69–70, பன்னாட்டுத் தரப்புத்தக எண்:9780867204759, http://books.google.com/books?id=B81gnTjNazMC&pg=PA69.
- Iannaccone, Andrew; Walden, Byron (2003), The Conformal Center of a Triangle or a Quadrilateral, Harvey Mudd College Department of Mathematics, http://www.math.hmc.edu/seniorthesis/archives/2003/aiannacc/aiannacc-2003-thesis.pdf.
- Johnson, Roger A. (1917), "Directed angles and inversion, with a proof of Schoute's theorem", American Mathematical Monthly 24 (7): 313–317.
- Clark Kimberling (1993), "Functional equations associated with triangle geometry", Aequationes Mathematicae 45 (2-3): 127–152, doi:10.1007/BF01855873.
- Moon, Tarik Adnan (2010), "The Apollonian circles and isodynamic points", Mathematical Reflections (6), http://awesomemath.org/wp-content/uploads/reflections/2010_6/Isodynamic_moon_c.pdf.
- Joseph Jean Baptiste Neuberg (1885), "Sur le quadrilatère harmonique" (in French), Mathesis (journal) 5: 202–204, 217–221, 265–269, http://books.google.com/books?ei=CdVoT4LIBIabiAL3gvCiBw&id=LhFOAAAAMAAJ. The definition of isodynamic points is in a footnote on page 204.
- Rigby, J. F. (1988), "Napoleon revisited", Journal of Geometry 33 (1-2): 129–146, doi:10.1007/BF01230612. The discussion of isodynamic points is on pp. 138–139. Rigby calls them "Napoleon points", but that name more commonly refers to a different triangle center, the point of concurrence between the lines connecting the vertices of Napoleon's equilateral triangle with the opposite vertices of the given triangle.
- Wildberger, N. J. (2008), "Neuberg cubics over finite fields", Algebraic geometry and its applications, Ser. Number Theory Appl., 5, World Sci. Publ., Hackensack, NJ, pp. 488–504, doi:10.1142/9789812793430_0027. See especially p. 498.
வெளியிணைப்புகள்
- Isodynamic points X(15) and X(16) in the Encyclopedia of Triangle Centers, by Clark Kimberling
- Eric W. Weisstein, Isodynamic Points MathWorld இல்.