பாத முக்கோணம்

பாத முக்கோணம் (pedal triangle) என்பது ஒரு முக்கோணத்தின் மூன்று பக்கங்களின் மீது ஒரு புள்ளியை வீழ்த்துவதன் மூலம் பெறப்படுகிறது.

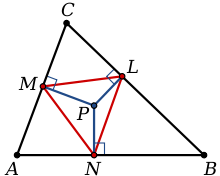
P -புள்ளியிலிருந்து முக்கோணம் ABC (கருப்பு) இன் பக்கங்களுக்கு வரையப்படும் செங்குத்துகளின் (நீலம்) அடிப்புள்ளிகளை இணைக்கக் கிடைக்கும் முக்கோணம் LMN (சிவப்பு) பாத முக்கோணம் ஆகும்.

முக்கோணம் ABC இன் பக்கங்களின் மீது P என்ற புள்ளியை வீழ்த்தும்போது, அதாவது P லிருந்து முக்கோணத்தின் ஒவ்வொரு பக்கத்திற்கும் செங்குத்துகள் வரையப்படும்பொழுது, அச்செங்குத்துகளின் அடிப்புள்ளிள் L, M, N எனில், இம்மூன்று புள்ளிகளையும் இணைத்து வரையப்படும் முக்கோணம் LMN பாத முக்கோணம் ஆகும்.

P புள்ளியைப் பொறுத்து பாத முக்கோணம் ABC முக்கோணத்தின் சில சிறப்புவகை முக்கோணங்களாகவும் அமையும்:

ABC முக்கோணத்தின் சுற்றுவட்டத்தின்மீது புள்ளி P அமையும்பொழுது பாத முக்கோணம் ஒரு கோடாக (சிவப்பு) அமைகிறது.
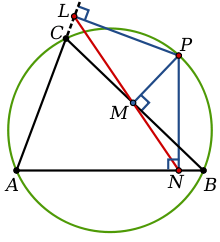
  • ABC முக்கோணத்தின் சுற்றுவட்டத்தின்மீது புள்ளி P அமையும்பொழுது பாத முக்கோணம் ஒரு கோடாகி விடுகிறது. இக்கோடு பாதக் கோடு (pedal line) என்றும் சில சமயங்களில் கணிதவியலாளர் ராபர்ட் சிம்சனின் பெயரால் சிம்சன் கோடு (Simson line) எனவும் அழைக்கப்படுகிறது.

மூல முக்கோணத்தின் உட்புறமாக அமையும் புள்ளி P இன் பாத முக்கோணத்தின் உச்சிகள் மூல முக்கோணத்தின் பக்கங்களைக் கீழே தரப்பட்டுள்ள முடிவை நிறைவு செய்யும் விதமாகப் பிரிக்கின்றன.[1]:85-86

முந்நேரியல் ஆட்கூறுகள்

புள்ளி P இன் முந்நேரியல் ஆட்கூறுகள் p : q : r எனில், பாத முக்கோணத்தின் உச்சிகள் L, M, N இன் முந்நேரியல் ஆட்கூறுகள்:

  • L = 0 : q + p cos C : r + p cos B
  • M = p + q cos C : 0 : r + q cos A
  • N = p + r cos B : q + r cos A : 0

எதிர்பாத முக்கோணம்

மூல முக்கோணம் ABC இன் உச்சிகளையும் புள்ளி P ஐயும் இணைக்கும் கோட்டுத்துண்டுகள் AP, BP, CP. இம்மூன்று கோட்டுத்துண்டுகள் ஒவ்வொன்றுக்கும் P லிருந்து வரையப்படும் செங்குத்துக்கோடுகள் மூன்றும் இரண்டிரண்டாக வெட்டிக்கொள்ளும் புள்ளிகள் (L ' M ' N ') மூன்றையும் இணைத்து வரையப்படும் முக்கோணமே P இன் எதிர்பாத முக்கோணம் ஆகும்.

எதிர்பாத முக்கோணத்தின் உச்சிகளின் முந்நேரியல் ஆட்கூறுகள்:

  • L' = − (q + p cos C)(r + p cos B) : (r + p cos B)(p + q cos C) : (q + p cos C)(p + r cos B)
  • M' = (r + q cos A)(q + p cos C) : − (r + q cos A)(p + q cos C) : (p + q cos C)(q + r cos A)
  • N' = (q + r cos A)(r + p cos B) : (p + r cos B)(r + q cos A) : − (p + r cos B)(q + r cos A)

எடுத்துக்காட்டு:

ஒரு முக்கோணத்தின்மூன்று வெளிவட்டமையங்களாலான முக்கோணமானது அந்த மூல முக்கோணத்தின் உள்வட்ட மையத்தின் எதிர்பாத முக்கோணமாக இருக்கும்.

முக்கோணத்தின் மூன்று பக்கங்கள் BC, CA, AB,க்களின்இன் நீட்டிப்புகளின் மீது புள்ளி P அமையாதநிலையில், P இன் சமகோண இணையியப் புள்ளி P−1 ஆக இருந்தால்,, P இன் பாத முக்கோணமானது P−1 இன் எதிர்பாத முக்கோணத்துடன் ஒத்தநிலை கொண்டதாயிருக்கும். ஒத்தநிலை மையத்தின் முந்நேரியல் ஆட்கூறுகள்:

ap(p + q cos C)(p + r cos B) : bq(q + r cos A)(q + p cos C) : cr(r + p cos B)(r + q cos A).

P ஒரு முக்கோண மையமாக "இருந்தால், இருந்தால் மட்டுமே" இந்த ஒத்தநிலை மையமும் ஒரு முக்கோண மையமாக இருக்கும்.

P இன் பாத முக்கோணம் மற்றும் P−1 இன் எதிர்பாத முக்கோணங்களின் பரப்பளவுகளின் பெருக்குத்தொகையானது மூல முக்கோணமான முக்கோணம் ABC இன் பரப்பளவின் வர்க்கத்திற்குச் சமமாக இருக்கும்..

மேற்கோள்கள்
  1. Alfred S. Posamentier and Charles T. Salkind, Challenging Problems in Geometry, Dover Publishing Co., second revised edition, 1996.

வெளியிணைப்புகள்
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.