எதிரொளிப்பு (கணிதம்)

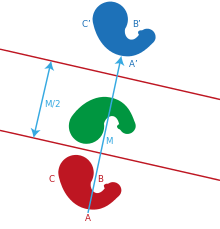
ஒரு தளத்தில் அமைந்த ஒரு புள்ளியின் எதிரொளிப்பு எதிருருவைக் காண, எடுத்துக்கொள்ளப்பட்ட புள்ளியிலிருந்து எதிரொளிப்பு அச்சுக்கு (தளம்) செங்குத்துக் கோடொன்று வரையவேண்டும். புள்ளிக்கும் எதிரொளிப்பு அச்சுக்கும் இடைப்பட்ட தூர அளவுவரை அச்செங்குத்துக் கோட்டினை எதிரொளிப்பு அச்சுக்கு எதிர்ப்புறம் நீட்டிக்க வேண்டும். நீட்டிக்கப்பட்ட கோட்டுத்துண்டின் இறுதிமுனையே எடுத்துக்கொள்ளப்பட்ட புள்ளியின் எதிரொளிப்பு எதிருரு ஆகும்.

ஒரு தளத்தில் அமைந்த ஒரு வடிவத்தின் எதிரொளிப்பு எதிருருவைக் காண்பதற்கு அவ்வடிவத்தின் ஒவ்வொரு புள்ளிக்கும் எதிருரு காணவேண்டும்.

ஒரு அச்சில் எதிரொளிப்பு நிகழ்ந்து, அதனைத் தொடர்ந்து முதல் எதிரொளிப்பு அச்சுக்கு இணையில்லாத மற்றொரு அச்சில் எதிரொளிக்கப்பட்டால் இரண்டு எதிரொளிப்புகளின் இணைந்த விளவானது சுழற்சி ஆகும்.

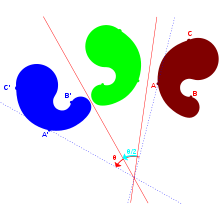
ஒரு எதிரொளிப்பின் அணி ஒரு செங்குத்து அணியாகும். அந்த அணியின் அணிக்கோவையின் மதிப்பு -1 ஆகவும், ஐகென் மதிப்புகள் (1, 1, 1, … 1, -1) ஆகவும் இருக்கும். இரு எதிரொளிப்புகளின் அணிகளின் பெருக்கல் ஒரு சிறப்புவகையான செங்குத்து அணியாக இருக்கும். மேலும் அந்த அணி சுழற்சியைக் குறிக்கும். ஆதியின் வழியாகச் செல்லும் மீத்தளங்களில் இரட்டை எண்ணிக்கையில் நிகழும் எதிரொளிப்புகளின் இணைந்த விளைவாகவே ஒவ்வொரு சுழற்சியும் அமைகிறது. இதேபோல ஒற்றை எண்ணிக்கையில் நிகழும் எதிரொளிப்புகளின் இணைந்த விளைவாகவே ஒவ்வொரு தகாசுழற்சியும் அமையும். எனவே எதிரொளிப்புகள் செங்குத்து குலத்தை உருவாக்குகின்றன.

இதேபோல, அனைத்து யூக்ளிடிய சம அளவை உருமாற்றங்களையும் கொண்ட யூக்ளிடிய குலமானது கேண்முறை மீத்தளங்களில் நடைபெறும் எதிரொளிப்புகளால் உருவாக்கப்படுகிறது. பொதுவாக, கேண்முறை மீத்தளங்களில் நிகழும் எதிரொளிப்புகளால் உருவாக்கப்படும் குலமானது எதிரொளிப்புக் குலம் என அழைக்கப்படுகிறது.

இருபரிமாணத்தில், ஆதி வழியாகச் செல்லும் ஒரு கோட்டில் நிகழும் எதிரொளிப்பின் வாய்ப்பாடு:

${\displaystyle \mathrm {Ref} _{l}(v)=2{\frac {v\cdot l}{l\cdot l}}l-v}$

v -எதிரொளிக்கப்படும் திசையன்;

l -எதிரொளிப்பு நிகழும் கோட்டிலமைந்த திசையன்;

v·l – v, l திசையன்களின் புள்ளிப் பெருக்கம்

இவ்வாய்ப்பாட்டினை கீழுள்ளவாறும் அமையும்:

${\displaystyle \mathrm {Ref} _{l}(v)=2\mathrm {Proj} _{l}(v)-v\,}$

ஒரு கோட்டில் நிகழும் எதிரொளிப்புகளின் ஐகென் மதிப்புகள்: 1, −1.

Rⁿ-யூக்ளிடிய வெளி; இதிலமைந்த திசையன் a ; இத்திசையனுக்கு செங்குத்தாக ஆதிவழியாகச் செல்லும் மீத்தளத்தில் நிகழும் எதிரொளிப்பு:

${\displaystyle \mathrm {Ref} _{a}(v)=v-2{\frac {v\cdot a}{a\cdot a}}a}$

v·a – v, a திசையன்களின் புள்ளிப்பெருக்கம்

• vஆனது a க்கு இணையெனில்,

Ref_a(v) = − v

• vஆனது a க்கு செங்குத்தெனில்,

Ref_a(v) = v

இந்த எதிரொளிப்புகளெல்லாம் யூக்ளிடிய சம அளவை உருமாற்றங்கள் என்பதால், ஆதியைத் தேர்ந்தெடுத்து நிலைப்படுத்துவதன் மூலம் இவற்றை செங்குந்து அணிகள் மூலம் குறிக்கலாம். மேலே தரப்பட்டுள்ள எதிரொளிப்பின் செங்குத்து அணியின் உறுப்புகள்:

${\displaystyle R_{ij}=\delta _{ij}-2{\frac {a_{i}a_{j}}{\|a\|^{2}}}}$

δ_ij -குரோனெக்கர் டெல்டா

ஆதி வழியாகச் செல்லாத கேண்முறை மீத்தளத்திலான (${\displaystyle v\cdot a=c}$ ) எதிரொளிப்பின் வாய்ப்பாடு:

${\displaystyle \mathrm {Ref} _{a,c}(v)=v-2{\frac {v\cdot a-c}{a\cdot a}}a.}$

• Harold Scott MacDonald Coxeter (1969), Introduction to Geometry (2nd ), New York: John Wiley & Sons, பன்னாட்டுத் தரப்புத்தக எண்:978-0-471-50458-0
• Vladimir L. Popov (2001), "Reflection", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, பன்னாட்டுத் தரப்புத்தக எண்:978-1556080104, http://www.encyclopediaofmath.org/index.php?title=R/r080510
• Weisstein, Eric W., "Reflection", MathWorld.

• Reflection in Line at cut-the-knot
• Understanding 2D Reflection and Understanding 3D Reflection by Roger Germundsson, The Wolfram Demonstrations Project.