நேர்மாற்ற வடிவவியல்

• 
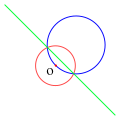  குறிப்பீட்டு வட்டத்தைப் (சிவப்பு) பொறுத்து அதன் மையம் O வழிச்செல்லும் மற்றொரு வட்டத்தின் (நீலம்) நேர்மாறானது O வழிச்செல்லாத ஒரு கோடாகும் (பச்சை).
• 
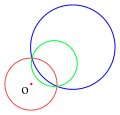  குறிப்பீட்டு வட்டத்தைப் (சிவப்பு) பொறுத்து அதன் மையம் O வழிச்செல்லாத மற்றொரு வட்டத்தின் (நீலம்) நேர்மாறானது O வழிச்செல்லாத ஒரு வட்டமாகும் (பச்சை).
• 
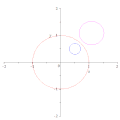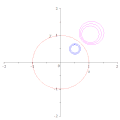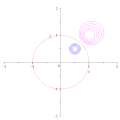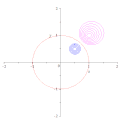  வட்ட நேர்மாற்றத்தால் ஒரு வட்டத்தின் மையத்தின் எதிருருவானது, எதிருரு வட்டத்தின் மையமாக அமைவதில்லை

ஒரு கணத்திலுள்ள எல்லாப் புள்ளிகளின் வட்ட நேர்மாற்ற எதிருருப் புள்ளிகள் எல்லாம் மற்றொரு கணமாக அமைகின்றன.

வட்ட நேர்மாற்றத்தைப் பயனுள்ளதாக்கும் சில பண்புகள் கீழே தரப்பட்டுள்ளன:

• குறிப்பீட்டு வட்டத்தின் மையம் O வழிச் செல்லும் ஒரு வட்டத்தின் வட்ட நேர்மாற்ற எதிருருவானது, O வழிச் செல்லாத, ஆனால் O இல் நேர்மாற்றத்துக்குட்படும் வட்டத்திற்கு வரையப்படும் தொடுகோட்டிற்கு இணையான கோடாக இருக்கும். மற்றும் இக்கூற்றின் எதிர்மாறுநிலையும் (vice versa) உண்மையாகும். (ஆனால் புள்ளிவாரியான நிலைப்பு இராது).[3]
• குறிப்பீட்டு வட்டத்தின் மையம் O வழிச் செல்லாத ஒரு வட்டத்தின் வட்ட நேர்மாற்ற எதிருருவானது, O வழிச் செல்லாத மற்றொரு வட்டமாகும். குறிப்பீட்டு வட்டமும் நேர்மாற்றமடையும் வட்டமும் வெட்டிக்கொள்ளும் இரண்டு புள்ளிகளும் நேர்மாற்றத்தில் நிலைப்பானவை. எனவே எதிருரு வட்டமானது இவ்விரு புள்ளிகளின் வழிச்செல்லும் வட்டமாக அமைகிறது. ஒரு வட்டமானது (அல்லது கோடு) குறிப்பீட்டு வட்டத்திற்கு, அவையிரண்டும் வெட்டும் புள்ளிகளில் செங்குத்தானதாக ‘இருந்தால், இருந்தால் மட்டுமே’ நேர்மாற்றத்தின்கீழ் நிலைப்பானதாக இருக்கும்.[3]
• k என்ற வட்டத்தைப் பொறுத்து நேர்மாறுகளாக அமையும் இரு வேறுபட்ட புள்ளிகள் A, A' . இவ்விரு புள்ளிகளின் வழியே செல்லும் மற்றொரு வட்டம் q எனில், வட்டங்கள் k , q இரண்டும் ஒன்றுக்குக்கொன்று செங்குத்து வட்டங்களாக இருக்கும்.
• முக்கோணம் OAB இல் உச்சி O ஆனது k வட்டத்தின் மையமாகவும், A' and B' இரண்டும் முக்கோணத்தின் உச்சிகள் A , B இன் k ஐப் பொறுத்த நேர்மாறுப் புள்ளிகளாவும் இருந்தால்:

${\displaystyle \angle OAB=\angle OB'A'\ {\text{ and }}\ \angle OBA=\angle OA'B'.}$

• k வட்டத்திற்கு செங்குத்து வட்டங்களாக அமையும் வட்டங்கள் p , q எனில், இவ்வட்டங்கள் இரண்டும் k வட்டத்தைப் பொறுத்து நேர்மாறுகளாக அமையும்.
• m , m' ஆகிய இரு வளைவரைகளின் மீதமையும் புள்ளிகள் M , M' இரண்டும் வட்டம் k ஐப் பொறுத்து நேர்மாறுகளெனில்,

M , M' புள்ளிகளில் m , m' வளைவரைகளுக்கு வரையப்படும் தொடுகோடுகள் MM' கோட்டிற்கு செங்குத்தாக அமையும். அல்லது MM' ஐ அடிப்பக்கமாகக் கொண்ட இருசமபக்க முக்கோணத்தினை அமைக்கும்.

• நேர்மாற்றத்தால் கோணங்களின் அளவுகள் மாற்றமடைவதில்லை; ஆனால் திசைப்போக்குடைய கோணங்களின் திசைப்போக்கு எதிராகிறது.[4]

• Altshiller-Court, Nathan (1925), College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle (2nd ), New York: Barnes & Noble
• Blair, David E. (2000), Inversion Theory and Conformal Mapping, American Mathematical Society, பன்னாட்டுத் தரப்புத்தக எண்:0-8218-2636-0
• Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1998), "Chapter 5: Inversive Geometry", Geometry, Cambridge: Cambridge University Press, pp. 199–260, பன்னாட்டுத் தரப்புத்தக எண்:0-521-59787-0
• Harold Scott MacDonald Coxeter (1969) [1961], Introduction to Geometry (2nd ), John Wiley & Sons, பன்னாட்டுத் தரப்புத்தக எண்:0-471-18283-4, http://books.google.com/books?id=c0ld-crynsIC
• Robin Hartshorne (2000), "Chapter 7: Non-Euclidean Geometry, Section 37: Circular Inversion", Geometry: Euclid and Beyond, Springer, பன்னாட்டுத் தரப்புத்தக எண்:0-387-98650-2, http://www.springer.com/mathematics/geometry/book/978-0-387-98650-0
• Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston

• Inversion: Reflection in a Circle at ”cut-the-knot”
• Wilson Stother's inversive geometry page
• IMO Compendium Training Materials practice problems on how to use inversion for math olympiad problems
• Weisstein, Eric W., "Inversion", MathWorld.
• Visual Dictionary of Special Plane Curves Xah Lee