கிட்டத்தட்ட நிறைவெண்

கணிதத்தில் கிட்டத்தட்ட நிறைவெண் (almost perfect number) என்பது அதன் அனைத்து வகுஎண்களின் கூட்டுத்தொகையானது அவ்வெண்ணின் இருமடங்கு மதிப்பில் ஒன்று குறைவாக உள்ள இயல் எண் ஆகும்.

குசெனைரின் கோல்கள் கொண்டு (Cuisenaire rod) எண் 8, ஒரு கிட்டத்தட்ட நிறைவெண் மற்றும் குறைவெண் எனக் காட்டப்படுகிறது.

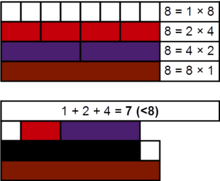
இயல் எண் n ஒரு கிட்டத்தட்ட நிறைவெண் எனில், n இன் அனைத்து வகுஎண்களின் கூட்டுத்தொகை 2n − 1 ஆக இருக்கும்.

அதாவது n இன் வகுஎண் சார்பு:

σ(n)) = 2n − 1.

n இன் தகு வகுஎண் சார்பு:

s(n) = σ(n) − n, = (2n − 1) - n = n − 1.

எதிரிலா அடுக்குகளைக் கொண்ட இரண்டின் அடுக்குகள் மட்டுமே கிட்டத்தட்ட நிறைவெண்களாக உள்ளன (OEIS-இல் வரிசை A000079) .

கண்டறியப்பட்டுள்ள கிட்டத்தட்ட நிறைவெண்களில்:

2⁰ = 1 மட்டும்தான் ஒற்றையெண்

k ஒரு நேர் எண் எனில், 2^k என்ற வடிவிலுள்ளவை மட்டும்தான் இரட்டையெண்களாகும்.

எனினும் கிட்டத்தட்ட நிறைவெண்கள் அனைத்தும் இதே வடிவில் அமைந்திருக்குமா என்பது அறியப்படவில்லை. ஒன்றைவிடப் பெரிய ஒற்றை கிட்டத்தட்ட நிறைவெண்கள் குறைந்தபட்சம் 6 பகாக்காரணிகளைக் கொண்டிருக்கும் எனக் கண்டறியப்பட்டுள்ளது.[1][2]

If m ஒரு ஒற்றை கிட்டத்தட்ட நிறைவெண் எனில், m(2m − 1) ஒரு டேக்கார்ட் எண் ஆக இருக்கும்.[3] மேலும் a , b இரண்டும் ${\displaystyle b+3<a<{\sqrt {m/2}}}$ என்றவாறான நேர் ஒற்றை முழுஎண்கள் மற்றும் 4m − a, 4m + b இரண்டும் பகாஎண்கள் எனில், m(4m − a)(4m + b) ஒரு ஒற்றை விந்தை எண்ணாக இருக்கும்.[4]