ஸ்பைக்கர் வட்டமையம்
ஸ்பைக்கர் வட்டமையம் (Spieker center), முக்கோண மையங்களுள் ஒன்றாகும். கிளார்க் கிம்பர்லியின் முக்கோண மையங்கள் கலைக்களஞ்சியத்தில் இப்புள்ளி X(10) எனப் பட்டியலிடப்பட்டுள்ளது. இது முக்கோணத்தின் சுற்றளவின் பொருண்மை மையமாக (center of mass) வரையறுக்கப்பட்டுள்ளது. முக்கோணம் ABCஇன் ஸ்பைக்கர் வட்டமையமானது அம்முக்கோண வடிவிலமைந்த கம்பிச்சட்டத்தின் திணிவு மையமாக இருக்கும்.[1][2] 19 ஆம் நூற்றாண்டின் செர்மானிய வடிவவியலாளர் தியோடர் ஸ்பைக்கரைச் சிறப்பிக்கும் விதமாக இப்புள்ளி ஸ்பைக்கர் வட்டமையம் என அழைக்கப்படுகிறது.[3]
அமைவிடம்
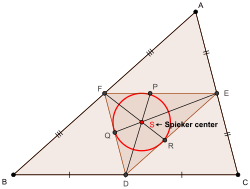
முக்கோணம் ABCஇன் ஸ்பைக்கர் வட்டமையமானது நடுப்புள்ளி முக்கோணத்தின் உள்வட்டமையம் ஆக இருப்பதைப் படத்தில் காணலாம்.
ஸ்பைக்கர் வட்டமையத்தை கீழ்க்காணும் இரு முடிவுகளைக் கொண்டு காணலாம்:
- முக்கோணம் ABCஇன் ஸ்பைக்கர் வட்டமையம், அம்முக்கோணத்தின் நடுப்புள்ளி முக்கோணத்தின் உள்வட்டமையமாக இருக்கும். அதாவது முக்கோணம் ABCஇன் நடுப்புள்ளி முக்கோணத்தினுள் அதன் பக்கங்களைத் தொடுமாறு வரையப்பட்ட வட்டத்தின் (ஸ்பைக்கர் வட்டம்) மையமாக இருக்கும். இம்முடிவைப் பயன்படுத்தி ஸ்பைக்கர் வட்டமையத்தைக் காணலாம்[1].
- ஒரு முக்கோணத்தின் வெட்டி என்பது முக்கோணத்தின் சுற்றளவை இருசமக்கூறிடும் கோட்டுத்துண்டாகும். இக்கோட்டுத்துண்டின் ஒரு முனை முக்கோணத்தின் ஒரு பக்கத்தின் நடுப்புள்ளியாக இருக்கும். முக்கோணத்தின் சுற்றளவின் பொருண்மை மையமானது மூன்று வெட்டிகளின் மீதும் அமைந்திருக்கும் என்பதால் மூன்று வெட்டிகளும் சந்திக்கும் புள்ளியானது பொருண்மை மையமாக, அதாவது ஸ்பைக்கர் மையமாக இருக்கும். இம்முடிவை பயன்படுத்தியும் ஸ்பைக்கர் வட்டமையத்தைக் காணலாம்.
பண்புகள்
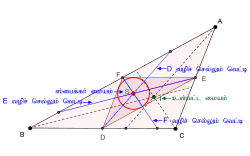
ஒரு முக்கோணத்தின் வெட்டிகள் சந்திக்கும்புள்ளியானது அம்முக்கோணத்தின் ஸ்பைக்கர் வட்டமையமாக உள்ளது.
முக்கோணம் ABCஇன் ஸ்பைக்கர் வட்டமையம் S எனில்:.
- S இன் முக்கோட்டு ஆள்கூறுகள்:
- ( bc (b + c), ca (c + a), ab (a + b)).[4]
- S இன் ஈர்ப்புமைய ஆள்கூறுகள் (barycentric coordinates):
- ( b + c, c + a, a + b ).[4]
- முக்கோணத்தின் மூன்று வெளிவட்டங்களின் சமதொடுகோட்டச்சுச் சந்தியாக S அமையும்.[5]
- S , முக்கோணத்தின் மூன்று வெட்டிகளின் சந்திப்புமையமாகும்.[1]
- ABC முக்கோணத்தின் [[உள்வட்டமையம் (I), நடுக்கோட்டுச்சந்தி (G), நாகெல் புள்ளி (M) ஆகிய மூன்று புள்ளிகளுடனும் S ஒரே கோட்டில் அமையும். மேலும்,
- IS = SM, IG = 2·GS, MG = 2·IG.[6]
மேற்கோள்கள்
- Honsberger, Ross (1995). Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Mathematical Association of America. பக். 3–4.
- Kimberling, Clark. "Spieker center". பார்த்த நாள் 5 May 2012.
- Spieker, Theodor (1888). Lehrbuch der ebenen Geometrie. Potsdam, Germany.
- Kimberling, Clark. "Encyclopedia of Triangle Centers". பார்த்த நாள் 5 May 2012.
- Odenhal, Boris (2010), [http://forumgeom.fau.edu/FG2010volume10/FG201006.pdf "Some triangle centers associated with the circles tangent to the excircles"], Forum Geometricorum 10: 35–40, http://forumgeom.fau.edu/FG2010volume10/FG201006.pdf
- A. Bogomolny. "Nagel Line from Interactive Mathematics Miscellany and Puzzles". பார்த்த நாள் 5 May 2012.
This article is issued from
Wikipedia.
The text is licensed under Creative
Commons - Attribution - Sharealike.
Additional terms may apply for the media files.