நாகெல் புள்ளி

வடிவவியலில் ஒரு முக்கோணத்தின் நாகெல் புள்ளி (Nagel point) என்பது அம்முக்கோணத்தின் ஒரு முக்கோண மையம் (ஒரு முக்கோணத்தில் அதன் அமைவிடம் மற்றும் அளவுகளால் மாறுபடாதவகையில் வரையறுக்கப்படும் புள்ளிகள் முக்கோண நடுப்புள்ளிகள்) ஆகும். முக்கோணம் ABC இன் வெளிவட்டங்களின் தொடுபுள்ளிகள் T_A, T_B, T_C எனில் AT_A, BT_B, CT_C ஆகிய மூன்று கோட்டுத்துண்டுகளும் முக்கோணத்தின் பிளப்பிகள்) ஆகும். அவை மூன்றும் ஒரு புள்ளியில் சந்திக்கின்றன. அப்புள்ளி முக்கோணத்தின் நாகெல் புள்ளி (N) எனப்படுகிறது. 19ஆம் நூற்றாண்டின் ஜெர்மானியக் கணிதவியலாளரான கிறிஸ்டியன் ஹெயின்ரிச் வொன் நாகலைச் (Christian Heinrich von Nagel) சிறப்பிக்கும் விதமாக இப்புள்ளிக்குப் அவரது பெயர் இடப்பட்டுள்ளது.

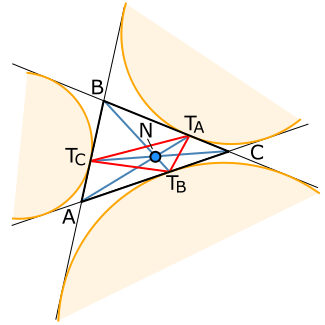
ABC முக்கோணத்தின் சிவப்புநிற முக்கோணம் வெளித்தொடு முக்கோணம். ஆரஞ்சுநிற வட்டங்கள், முக்கோணம் ABC இன் வெளிவட்டங்கள். அவை முக்கோணத்தின் பக்கங்களைச் சந்திக்கும் புள்ளிகள் T_A, T_B, T_C. கோட்டுத்துண்டுகள் AT_A, BT_B, and CT_C மூன்றும் சந்திக்கும் புள்ளி ABC முக்கோணத்தின் நாகெல் புள்ளி -N (நீலம்)

வெளிவட்டங்களின் துணையின்றியும் T_A, T_B, T_C புள்ளிகளைக் காணலாம். A இலிருந்து முக்கோணத்தின் வரம்பு வழியே முக்கோணத்தின் அரைச்சுற்றளவு தொலைவில் T_A புள்ளியும், B இலிருந்து முக்கோணத்தின் வரம்பு வழியே முக்கோணத்தின் அரைச்சுற்றளவு தொலைவில் T_B புள்ளியும், C இலிருந்து முக்கோணத்தின் வரம்பு வழியே முக்கோணத்தின் அரைச்சுற்றளவு தொலைவில் T_C புள்ளியும் அமைகின்றன. இதனால் நாகெல் புள்ளியானது இருசமக்கூறிடப்பட்ட சுற்றளவுப் புள்ளி (bisected perimeter point) எனவும் சில சமயங்களில் அழைக்கப்படுகிறது.,

பிற முக்கோண மையங்களுடன் தொடர்பு

நாகெல் புள்ளியானது கெர்கோன் புள்ளியின் ஐசோட்டாமிக் இணையியம் ஆகும். ஒரு முக்கோணத்தின் நாகெல் புள்ளி, நடுக்கோட்டுச்சந்தி, உள்வட்ட மையம் ஆகிய மூன்றும் ஒரே கோட்டின் மீதமைகின்றன. அக்கோடு, "நாகெல் கோடு" எனப்படுகிறது. நடுப்புள்ளி முக்கோணத்தின் நாகெல் புள்ளியாக உள்வட்ட மையம் இருக்கும்.[1][2]

முக்கோட்டு ஆட்கூறுகள்

நாகெல் புள்ளியின் முக்கோட்டு ஆட்கூறுகள் (trilinear coordinates)[3]:

\csc ^{2}(A/2)\,:\,\csc ^{2}(B/2)\,:\,\csc ^{2}(C/2)

(அல்லது)

முக்கோணத்தின் பக்க நீளங்கள் a = |BC|, b = |CA|, and c = |AB| எனில்:

{\frac {b+c-a}{a}}\,:\,{\frac {c+a-b}{b}}\,:\,{\frac {a+b-c}{c}}.

மேற்கோள்கள்

Anonymous (1896). Problem 73. "Geometry: 69-72". American Mathematical Monthly 3 (12): 329.
"Why is the Incenter the Nagel Point of the Medial Triangle?".
Gallatly, William (1913). The Modern Geometry of the Triangle (2nd ). London: Hodgson. பக். page 20.

Baptist, Peter (1987). "Historische Anmerkungen zu Gergonne- und Nagel-Punkt". Sudhoffs Archiv für Geschichte der Medizin und der Naturwissenschaften 71 (2): 230–233.

வெளியிணைப்புகள்

Nagel Point from Cut-the-knot
Nagel Point, Clark Kimberling
Eric W. Weisstein, Nagel Point MathWorld இல்.
Spieker Conic and generalization of Nagel line at Dynamic Geometry Sketches Generalizes Spieker circle and associated Nagel line.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Anonymous-1] Anonymous (1896). Problem 73. "Geometry: 69-72". American Mathematical Monthly 3 (12): 329.

[2] "Why is the Incenter the Nagel Point of the Medial Triangle?".

[Gallatly-3] Gallatly, William (1913). The Modern Geometry of the Triangle (2nd ). London: Hodgson. பக். page 20.