படிநிலைச் சார்பு
கணிதத்தில் மெய்யெண்களின் மீது வரையறுக்கப்பட்ட ஒரு சார்பினை, இடைவெளிகளின் சுட்டுச் சார்புகளின் முடிவுறு நேரியல் சேர்வாக எழுத முடியுமானால் அச்சார்பு படிநிலைச் சார்பு (step function) என அழைக்கப்படுகிறது. இச்சார்பு படிக்கட்டுச் சார்பு (staircase function) என்றும் அழைக்கப்படுகிறது. முடிவுறு துண்டுகளைக் கொண்ட துண்டுவாரி மாறிலிச் சார்பாகவும் ஒரு படிநிலைச் சார்பினைக் கருதலாம்.
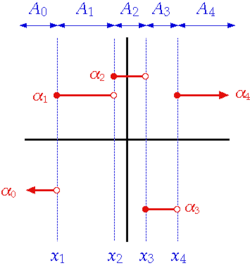
வரையறை
என்ற சார்பு கீழ்க்காணுமாறு எழுதக் கூடியதானால் அது ஒரு படிநிலைச் சார்பாக இருக்கும்.
- ,
- -இடைவெளிகள்
- (சிலசமயங்களில் ) இன் சுட்டுச் சார்பு:
இந்த வரையறையில் காணும் இடைவெளிகளை பின்வரும் பண்புகளைக் கொண்டவையாய்க் கொள்ளலாம்:
- எடுத்துக்கொள்ளப்படும் அனைத்து இடைவெளிகளும் சேர்ப்பில்லாக் கணங்கள். அதாவது, for
- அவை அனைத்தின் கணம் (கணிதம்)#ஒன்றுப்புகள்ஒன்றிப்பு முழுமையான மெய்யெண் கோடாக இருக்கும்.
இவ்விரு பண்புகளைக் கொண்ட இடைவெளிகளாக இல்லாமல் இருந்தாலும் நாம் வேறுசில இடைவெளிகளை இணைத்துக் கொள்வதன் மூலம் இவை உண்மையாக இருக்குமாறு செய்து கொள்ளலாம்.
எடுத்துக்காட்டு:
- -இப்படிநிலைச் சார்பை பின்வருமாறு மாற்றி எழுத, அதில் வரும் இடைவெளிகள் மேலே குறிப்பிடப்பட்ட இரு பண்புகளையும் கொண்டவையாக அமைவதைக் காணலாம்.
எடுத்துக்காட்டுகள்
- மாறிலிச் சார்பு (இதிலுள்ள ஒரே இடைவெளி: )
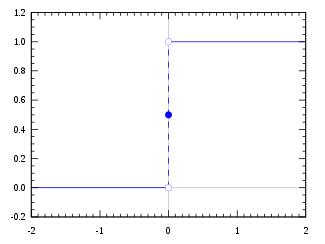
- ஹீவிசைட் படிநிலைச் சார்பு (படிநிலைச் சார்புகளில் முக்கியமானது.)
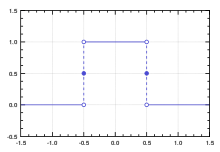
- செவ்வகச் சார்பு
படிநிலைச் சார்பல்லாதவை
- இவ்வரையறையின் படி முழுஎண்பகுதிச் சார்புக்கு முடிவுறா எண்ணிக்கையிலான இடைவெளிகள் உள்ளதால் அச்சார்பு ஒரு படிநிலைச் சார்பாகாது. முடிவுறா எண்ணிகையிலான இடைவெளிகளைக் கொண்டும் படிநிலைச் சார்பானது சில நூலாசிரியர்களால் வரையறுக்கப்படுகிறது.[1]
பண்புகள்
- இரு படிநிலைச் சார்புகளின் கூடுதல் மற்றும் பெருக்கல் சார்புகள் இரண்டுமே படிநிலைச் சார்புகளாகும்; ஒரு படிநிலைச் சார்பினை ஒரு எண்ணால் பெருக்கக் கிடைக்கும் சார்பும் ஒரு படிநிலைச் சார்பாகவே இருக்கும்.
- ஒரு படிநிலைச் சார்பு முடிவுறு எண்ணிக்கையிலான மதிப்புகளைக் கொண்டிருக்கும்:
மேலே தரப்பட்ட படிநிலைச் சார்பின் வரையறையில், இடைவெளிகள் எல்லாம் ஒன்றுக்கொன்று சேர்ப்பில்லாக் கணங்களாகவும் அவற்றின் மொத்த ஒன்றிப்பும் முழு மெய்யெண் கோடாகவும் இருந்தால்,
- ,
மேற்கோள்கள்
- for example see: Bachman, Narici, Beckenstein. "Example 7.2.2". Fourier and Wavelet Analysis. Springer, New York, 2000. பன்னாட்டுத் தரப்புத்தக எண்:0-387-98899-8.