துண்டுவாரிச் சார்பு
கணிதத்தில் துண்டுவாரியாக வரையறுக்கப்பட்டச் சார்பு அல்லது துண்டுவாரிச் சார்பு (piecewise-defined function அல்லது piecewise function) என்பது பல உட்சார்புகளாக வரையறுக்கப்பட்டதொரு சார்பு. இந்த உட்சார்புகளின் ஆட்களங்கள், மூலச் சார்பின் ஆட்களத்தின் உட்கணங்களாக இருக்கும். ஒரு சார்பு துண்டுவாரியாக வரையறுக்கப்படும்போது அதன் தன்மையை அறிந்து கொள்ள முடிகிறது. ஒரு துண்டுவாரி பல்லுறுப்புக்கோவைச் சார்பானது, அதன் தனித்தனியான உள் ஆட்களங்களில் வரையறுக்கப்பட்ட வெவ்வேறான பல்லுறுப்புக்கோவைகளால் ஆனதாக அமையும்.
ஒரு துண்டுவாரியாக வரையறுக்கப்பட்ட சார்பின் குறிப்பிட்ட உள் ஆட்களங்களில் மட்டும் அச்சார்பு கொண்டிருக்கும் பண்புகளை விளக்கவும் துண்டுவாரி என்ற சொல் பயன்படுத்தப்படலாம். ஒரு சார்பு அதன் ஒவ்வொரு துண்டிற்குரிய உள் ஆட்களங்களம் முழுவதும் வகையிடத்தக்கதாக இருந்தால் அச்சார்பு துண்டுவாரியாக வகையிடத்தக்கது அல்லது துண்டுவாரியாக தொடர்ச்சியாக வகையிடத்தக்கது எனப்படும். இங்கு துண்டுகளுக்கு இடைப்பட்ட புள்ளிகளில் முழுச் சார்பானது வகையிடத்தக்கதாய் இருக்கவேண்டியதில்லை. குவிவுப் பகுப்பாய்வியலில் வகைக்கெழுக்களுக்குப் பதிலாக உள் வகைக்கெழுக்கள் கணக்கில் கொள்ளப்படுகின்றன. துண்டுவாரி வரையறையில் துண்டுகள் என்பது இடைவெளிகளாகவே எப்பொழுதும் இருப்பதில்லை. எனினும் அவை இடைவெளிகளாக இருக்கும்போது மட்டுமே அச்சார்புகள், துண்டுவாரி நேரியல் சார்புகள், துண்டுவாரித் தொடர்ச்சியானவை, துண்டுவாரி வகையிடத்தக்கவை என்று அழைக்கப்படுகின்றன.
குறியீடும் விளக்கமும்
சாதாரணச் சார்பின் குறியீடுகளைக் கொண்டு துண்டுவாரிச் சார்புகள் வரையறுக்கப்படுகின்றன. அதன் அமைப்பில் சார்பின் வரையறைகளும் அதற்குரிய உள் ஆட்களங்களும் வரிசையாக தரப்பட்டிருக்கும். உள் ஆட்களங்களின் எண்ணிக்கை முடிவுறு எண்ணாகவும் இடைவெளிகளாகவும் இருக்க வேண்டும்.
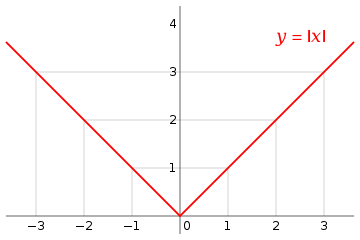
எடுத்துக்காட்டாக தனிமதிப்புச் சார்பின் வரையறை:
தனிமதிப்புச் சார்பின் வரையறையில்
- பூச்சியத்திற்கும் குறைவான x மதிப்புகளுக்கு, சார்பலன் (−x) என்பதால் உள்ளீடாகத் தரப்படும் எண்களின் சார்பலன் குறி மட்டும் எதிராக்கப்பட்ட அதே எண்ணாக இருக்கும்.
அதாவது, f (-3) = - (-3) = 3.
- பூச்சியம் மற்றும் பூச்சியத்திற்கும் அதிகமான x மதிப்புகளுக்கு, சார்பலன் (x) என்பதால் உள்ளீடாகத் தரப்படும் எண்கள் சார்பின் தாக்கத்தால் மாறுவதில்லை.
அதாவது f (3) = 3.
x இன் சில மதிப்புகளும் அவற்றுக்கான சார்பலன்களும் கீழே அட்டவணையாகத் தரப்பட்டுள்ளது:
| x | f(x) | பயன்படுத்தப்படும் சார்பு |
|---|---|---|
| −3 | 3 | −x |
| −0.1 | 0.1 | −x |
| 0 | 0 | x |
| 1/2 | 1/2 | x |
| 5 | 5 | x |
எனவே ஒரு குறிப்பிட்ட உள்ளீட்டிற்கான, ஒரு துண்டுவாரிச் சார்பின் மதிப்பைக் காண அதற்குரிய சரியான உள் ஆட்களத்தைத் தேர்ந்தெடுப்பது அவசியம்.
தொடர்ச்சி
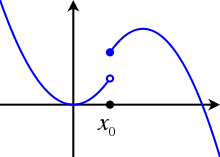
ஒரு துண்டுவாரிச் சார்பு, அதன் முழு ஆட்களமான இடைவெளியில் தொடர்ச்சியானதாக இருக்கப் பின்வரும் நிபந்தனைகள நிறைவு செய்யப்பட வேண்டும்:
- அந்த இடைவெளி முழுவதும் அச்சார்பு வரையறுக்கப்பட்டிருக்க வேண்டும்.
- அதன் கூறுச் சார்புகள் அவற்றின் உள் ஆட்களங்களில் தொடர்ச்சியானவை.
- அதன் இடைவெளியிலுள்ள உள் ஆட்களங்களின் ஒவ்வொரு முனைப்புள்ளிகளிலும் தொடர்ச்சியில்லாமல் இருத்தல் கூடாது.
படத்தில் தரப்பட்டுள்ள சார்பு, அதன் உள் ஆட்களங்களில் எல்லாம் துண்டுவாரியாக தொடர்ச்சியானதாக உள்ளது. எனினும் முழு ஆட்களத்தின் மீது தொடர்ச்சியானது இல்லை. இச்சார்பு புள்ளியில் துள்ளும் தொடர்ச்சியின்மை கொண்டுள்ளது.