Trabecula
A trabecula (plural trabeculae, from Latin for "small beam") is a small, often microscopic, tissue element in the form of a small beam, strut or rod that supports or anchors a framework of parts within a body or organ.[1][2] A trabecula generally has a mechanical function, and is usually composed of dense collagenous tissue (such as the trabecula of the spleen). They can be composed of other materials such as muscle and bone. In the heart, muscles form trabeculae carneae and septomarginal trabecula.[3] Cancellous bone is formed from groupings of trabeculated bone tissue.
| Trabecula | |
|---|---|
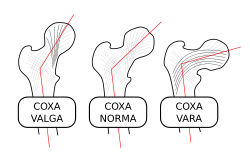 Alternation of trabecular pattern in the thigh bone reflects mechanical stress | |
| Details | |
| Part of | Bone |
| Identifiers | |
| FMA | 85273 |
| Anatomical terminology | |

In cross sections, trabeculae of a cancellous bone can look like septa, but in three dimensions they are topologically distinct, with trabeculae being roughly rod or pillar-shaped and septa being sheet-like.
When crossing fluid-filled spaces, trabeculae may have the function of resisting tension (as in the penis, see for example trabeculae of corpora cavernosa and trabeculae of corpus spongiosum) or providing a cell filter (as in the trabecular meshwork of the eye).
Multiple perforations in a septum may reduce it to a collection of trabeculae, as happens to the walls of some of the pulmonary alveoli in emphysema.
Structure
Trabecular bone, also called cancellous bone, is porous bone composed of trabeculated bone tissue. It can be found at the ends of long bones like the femur, where the bone is actually not solid but is full of holes connected by thin rods and plates of bone tissue.[4] Red bone marrow, where all the blood cells are made, fills the space between the trabecular pores. Even though trabecular bone contains a lot of holes, its spatial complexity contributes the maximal strength with minimum mass. It is noted that the form and structure of trabecular bone are organized to optimally resist loads imposed by functional activities, like jumping, running and squatting. And according to the famous Wolff's Law, proposed in 1892, the external shape and internal architecture of bone are determined by the external stresses acting on it.[5] The internal structure of the trabecular bone firstly undergoes adaptive changes along stress direction and then the external shape of cortical bone undergoes secondary changes. Finally bone structure becomes thicker and denser to resist the external loading.
Because of increasing amount of total joint replacement and its impact on bone remodeling, understanding the stress-related and adaptive process of trabecular bone has become a central concern for bone physiologists. In order to understand the role of trabecular bone in age-related bone structure and design for bone-implant system, it is significant to study the mechanical properties of trabecular bone as a function of variables, such as anatomic site, density and age. To do so, mechanical factors including modulus, uniaxial strength, and fatigue properties are necessary to be studied.
Typically, the porosity percent of trabecular bone is in the range 75–95% and the density ranges from 0.2 to 0.8g/cm3.[6] It is noted that the porosity can reduce the strength of the bone, but also reduce its weight. The porosity and the manner that porosity is structured affect the strength of material. Thus, the micro structure of trabecular bone is typically oriented and ''grain'' of porosity is aligned in a direction at which mechanical stiffness and strength are greatest. Because of the microstructual directionality, the mechanical properties of trabecular bone is highly an-isotropic. The range of young's modulus for trabecular bone is 800-14000 MPa and the strength of failure is 1-100 MPa.
As mentioned above, the mechanical properties of trabecular bone are very sensitive to apparent density. The relationship between modulus of trabecular bone and its apparent density was demonstrated by Carter and Hayes in 1976.[7] The resulting equation states:
where represents the modulus of trabecular bone in any loading direction, represents the apparent density, and and are constants depending on the architecture of tissue.
Additionally, from scanning electron microscopy, it was found that the variation in trabecular architecture with different anatomic sites lead to different modulus. To understand structure-anisotropy and material property relations, one must correlate the measured mechanical properties of anisotropic trabecular specimens with the stereologic descriptions of their architecture.[5]
The compressive strength of trabecular bone is also very important because it is believed that the inside failure of trabecular bone arise from compressive stress. On the stress-strain curves for both trabecular bone and cortical bone with different apparent density, there are three stage in stress-strain curve. The first one is linear region where individual trabecula bend and compress as the bulk tissue is compressed.[5] The second stage is after yielding, trabecular bonds start to fracture and the third stage is the stiffening stage. Typically, lower density trabecular areas have more deformed stage before stiffening than higher density specimens.[5]
In summary, trabecular bone is very compliant and heterogeneous. The heterogeneous character makes it difficult to summarize the general mechanical properties for trabecular bone. High porosity makes trabecular bone compliant and large variations in architecture leads to high heterogeneity. The modulus and strength vary inversely with porosity and highly depend on the porosity structure. Additionally, the effects of aging and small cracks of trabecular bones on their mechanical properties will be analyzed more in final drafts.
Clinical significance
.jpg)
Studies have shown that once a human reaches adulthood, bone density steadily decreases with age, to which loss of trabecular bone mass is a partial contributor.[8] Loss of bone mass is defined by the World Health Organization as osteopenia if bone mineral density (BMD) is one standard deviation below mean BMD in young adults, and is defined as osteoporosis if it is more than 2.5 standard deviations below the mean.[9] A low bone density greatly increases risk for stress fracture, which can occur without warning in those at risk.[10] The resulting low-impact fractures from osteoporosis most commonly occur in the upper femur, which consists of 25-50% trabecular bone depending on the region, in the vertebrae which are about 90% trabecular, or in the wrist.[11]
When trabecular bone volume decreases, its original plate-and-rod structure is disturbed; plate-like structures are converted to rod-like structures, and pre-existing rod-like structures thin until they disconnect and resorb into the body.[11] Changes in trabecular bone are typically gender-specific, with the most notable differences in bone mass and trabecular microstructure occurring within the age range for menopause.[8] Trabeculae degradation over time causes a decrease in bone strength that is disproportionately large in comparison to volume of trabecular bone loss, leaving the remaining bone vulnerable to fracture.[11]
With osteoporosis there are often also symptoms of osteoarthritis, which occurs when cartilage in joints is under excessive stress and degrades over time, causing stiffness, pain, and loss of movement.[12] With osteoarthritis, the underlying bone plays a significant role in cartilage degradation; thus any trabecular degradation can significantly affect stress distribution and adversely affect the cartilage in question.[13]
Due to its strong effect on overall bone strength, there is currently strong speculation that analysis in patterns of trabeculae degradation may be useful in the near-future in tracking the progression of osteoporosis.[14]
Birds
The hollow design of bird bones is multifunctional by establishing high specific strength and supplementing open airways to accommodate the skeletal pneumaticity common to many birds. The specific strength and resistance to buckling is optimized through their bone design that combines a thin, hard shell that encases a spongy core of trabeculae.[15] The allometry of their trabeculae allows the skeleton to tolerate loads without significantly increasing the bone mass.[16] The Red-Tailed Hawk optimizes its weight with a repeating pattern of V-shaped struts that give the bones the necessary lightweight and stiff characteristics. The inner network of trabeculae shifts mass away from the neutral axis, which ultimately increases the resistance to buckling.[15]
Just like in humans, the distribution of trabeculae in bird species is uneven, depending on the loading conditions. The bird with the highest density of trabeculae is the kiwi, a flightless bird.[16] There is also uneven distribution of trabeculae within the similar species such as the great spotted woodpecker or grey-headed woodpecker. After examining a microCT scan of the woodpecker's forehead, temporomandibulum, and occiput it was determined that there is significantly more trabeculae in the forehead and occiput.[17] Besides the difference in distribution, the aspect ratio of the individual struts was higher in woodpeckers than in other birds of similar size such as the Eurasian Hoopoe[17] or the lark.[18] The woodpeckers’ trabeculae are more plate-like while the hawk and lark have rod-like structures networked through their bones. The decrease in strain on the woodpecker's brain has been attributed to the higher quantity of thicker plate-like struts packed more closely together than the hawk or hoopoe or the lark.[18] Conversely, the thinner rod-like structures would lead to greater deformation. A destructive mechanical test with 12 samples show the woodpecker's trabeculae design has an average ultimate strength of 6.38MPa, compared to the lark's 0.55MPa.[17]
Besides the skull, the beak of woodpeckers have tiny struts supporting the shell of their beak, but to a lesser extent compared to their skull. As a result of less trabeculae in the beak, it has a higher stiffness of 1.0 GPa compared to the skull, 0.31 GPa. While the beak absorbs some of the impact from pecking, most of the impact is transferred to the skull where more trabeculae are actively available to absorb the shocks. The ultimate strength of the woodpecker's beak and lark's are similar, which can be inferred that the beak has a lesser role in impact absorption.[18] But one measured advantage of the woodpecker's beak is the slight overbite (upper beak is 1.6mm longer than lower beak) that causes a bimodal distribution of force due to the top beak contacting the surface moments before the bottom half of the beak. This staggered timing of impact induced a lower strain on the trabeculae in the forehead, occiput, and beak, than if the upper and lower beak had equal lengths.[19]
Research
Helmet technology
An important cause of injury and death is head injury. Scientists have been inspired by woodpeckers to advance helmet technology after learning about their ability to decelerate at 1,000 times the force of gravity continuously for an average of 15 pecks.[19] It is estimated that the woodpecker drums its beak approximately 12,000 times per day. It is assumed that the woodpeckers do not suffer any brain damage at these forces that immensely exceed the human capacity. A company called Riddell, a manufacturer of helmets for the United States Army and American football, is developing helmets to mitigate the stress on the front of the brain in a design similar to some birds.
Black box
Improvements to the impact strength of black boxes are being designed based on the head of a woodpecker. They consist of hard layers of steel and aluminum to mimic their beak and skull, an elastomeric component to uniformly disperse vibrations away from the skull like the hyoid bone , and a porous structure made of glass microspheres to dampen vibrations like trabecular bone. This structure survived a test up to 60,000 Gs.
Trabecular metal material
Created by Zimmer Biomet, Trabecular Metal material has been used clinically for 19 years for orthopedic applications such as implantations for the hip, knee, or shoulder as well as bone void fillers, osteonecrosis rods, and dental implants. It is an open-cell metal foam with up to 80% porosity, each pore size is on average 440 micrometers. It has a low stiffness and a high coefficient of friction of 0.98 so the implants remain secure without sliding. It is made of pure tantalum because it chemically inert, corrosion-resistant, and biocompatible. This trabecular structure has a high compressive modulus and high fatigue strength to withstand normal physiological stresses over long periods of time.[20]
Trabecula in other organisms
The larger the animal is, the higher the load its bones must withstand. Trabecular bone has previously been known to increase stiffness by increasing the amount of bone per unit volume or by altering the geometry and arrangement of individual trabeculae as body size and bone loading increases. Trabecular bone scales allometrically, reorganizing the bones’ internal structure to increase the ability of the skeleton to sustain loads experienced by the trabeculae. Furthermore, scaling of trabecular geometry can potentially moderate trabecular strain. Load acts as a stimulus to the trabecular, changing its geometry so as to sustain or mitigate strain loads. By using finite element modelling, a study tested four different species under an equal apparent stress (σapp) to show that trabecular scaling in animals alters the strain within the trabecular. It was observed that the strain within trabeculae from each species varied with the geometry of the trabeculae. From a scale of tens of micrometers, which is approximately the size of osteocytes, the figure below shows that thicker trabeculae exhibited less strain. The relative frequency distributions of element strain experienced by each species shows a higher elastic moduli of the trabeculae as the species size increases.
Additionally, trabeculae in larger animals are thicker, further apart, and less densely connected than those in smaller animals. Intra-trabecular osteon can commonly be found in thick trabeculae of larger animals, as well as thinner trabeculae of smaller animals such as cheetah and lemurs. The osteons play a role in the diffusion of nutrients and waste products in and out osteocytes by regulating the distance between osteocytes and bone surface to approximately 230 μm.
Due to an increased reduction of blood oxygen saturation, animals with high metabolic demands tend to have a lower trabecular thickness (Tb.Th) because they require increased vascular perfusion of trabeculae. The vascularization by tunneling osteons changes the trabecular geometry from solid to tube-like, increasing bending stiffness for individual trabeculae and sustaining blood supply to osteocytes that are embedded deep in the tissue.
Bone volume fraction (BV/TV) was found to be relatively constant for the variety of animal sizes tested. Larger animals did not show a significantly larger mass per unit volume of trabecular bone. This may be due to an adaptation which reduces the physiological cost of producing, maintaining, and moving tissue. However, BV/TV showed significant positive scaling in avian femoral condyles. Larger birds present decreased flight habits due to avian BV/TV allometry. The flightless kiwi, weighing only 1–2 kg, had the greatest BV/TV of the birds tested in the study. This shows that trabecular bone geometry is related to ‘prevailing mechanical conditions’, so the differences in trabecular geometry in the femoral head and condyle could potentially present the different loading environments of the coxofemoral and femorotibial joints.
The woodpecker’s ability to resist repetitive head impact is correlated with its unique micro/nanohierarchical composite structures. [18] Microstructure and nanostructure of the woodpecker’s skull consists of an uneven distribution of spongy bone, the organizational shape of individual trabeculae. This affects the woodpecker's mechanical properties, allowing the cranial bone to withstand a high ultimate strength (σu). Compared to the cranial bone of the lark, the woodpecker cranial bone is denser and less spongy, having a more plate-like structure to a more rod-like structure that is observed in larks. Furthermore, the woodpecker's cranial bone has a greater thickness and amount of individual trabeculae. Relative to the trabeculae in lark, the woodpecker’s trabecular is more closely spaced and more plate-like. [19] These properties result in a higher ultimate strength in the cranial bone of the woodpecker, than of the lark.
History
Diminutive form of Latin trabs, which means a beam or bar. In the 19th century, the neologism trabeculum (with an assumed plural of trabecula) became popular, but is less etymologically correct. Trabeculum persists in some countries as a synonym for the trabecular meshwork of the eye, but this can be considered poor usage on the grounds of both etymology and descriptive accuracy.
Other uses
For the skull development component, see trabecular cartilage.
References
- "Definition of TRABECULA". www.merriam-webster.com. Retrieved 2017-09-24.
- "trabecula". The Free Dictionary.
- Goo, Soyeon; Joshi, Purva; Sands, Greg; Gerneke, Dane; Taberner, Andrew; Dollie, Qaasim; LeGrice, Ian; Loiselle, Denis (October 2009). "Trabeculae carneae as models of the ventricular walls: implications for the delivery of oxygen" (PDF). The Journal of General Physiology. 134 (4): 339–350. doi:10.1085/jgp.200910276. ISSN 0022-1295. PMC 2757768. PMID 19752188.
- "Trabeculae of Bone: Definition & Function". Study.com. Retrieved 31 March 2017.
- Hayes, Wilson C.; Keaveny, Tony M. (1993). Bone: A Treatise (7 ed.). CRC Press. pp. 285–344. ISBN 978-0849388279. Retrieved 31 March 2017.
- Meyers, M. A.; Chen, P.-Y. (2014). Biological Materials Science. Cambridge: Cambridge University Press. ISBN 978-1-107-01045-1.
- Carter, D. R.; Hayes, W. C. (1976-12-10). "Bone compressive strength: the influence of density and strain rate". Science. 194 (4270): 1174–1176. doi:10.1126/science.996549. ISSN 0036-8075. PMID 996549.
- Parkinson, Ian H.; Fazzalari, Nicola L. (12 January 2012). Characterisation of Trabecular Bone Structure. Adelaide, SA, Australia: Springer-Verlag Berlin Heidelberg. pp. 31–51. ISBN 9783642180521. Retrieved 31 March 2017.
- "World Health Organization – WHO Criteria for Diagnosis of Osteoporosis". 4BoneHealth. Retrieved 31 March 2017.
- "Stress Fractures of the Foot and Ankle-OrthoInfo - AAOS". orthoinfo.aaos.org. Retrieved 31 March 2017.
- Wehrli, Felix W. "Role of Cortical and Trabecular Bone Architecture in Osteoporosis" (PDF). University of Pennsylvania School of Medicine. Retrieved 31 March 2017.
- Haq, I.; Murphy, E.; Dacre, J. (1 July 2003). "Osteoarthritis". Postgraduate Medical Journal. 79 (933): 377–383. doi:10.1136/pmj.79.933.377. ISSN 0032-5473. PMC 1742743. PMID 12897215. Retrieved 31 March 2017.
- Lorna, Gibson. "Lecture 11: Trabecular Bone and Osteoporosis | Video Lectures | Cellular Solids: Structure, Properties and Applications | Materials Science and Engineering | MIT OpenCourseWare". ocw.mit.edu. Massachusetts Institute of Technology. Retrieved 31 March 2017.
- Shetty, Aditya. "Trabecular pattern of proximal femur | Radiology Reference Article | Radiopaedia.org". radiopaedia.org. Retrieved 31 March 2017.
- Meyers, M. A.; Chen, P.-Y. (2014). Biological Materials Science. Cambridge: Cambridge University Press. pp. 504–506. ISBN 978-1-107-01045-1.
- Doube, Michael; et al. (2011). "Trabecular bone scales allometrically in mammals and birds". Proceedings of the Royal Society. B. 278 (1721): 3067–3073. doi:10.1098/rspb.2011.0069. PMC 3158937. PMID 21389033.
- Wang, Lizheng; et al. (2013). "Effect of Microstructure of Spongy Bone in Different Parts of Woodpecker's Skull on Resistance to Impact Injury". Journal of Nanomaterials. 2013: 1–6. doi:10.1155/2013/924564.
- Wang, L.; Zhang, H.; Fan, Y. (2011). "Comparative study of the mechanical properties, micro-structure, and composition of the cranial and beak bones of the great spotted woodpecker and the lark bird". Science China Life Sciences. 54 (11): 1036–1041. doi:10.1007/s11427-011-4242-2. PMID 22173310.
- Wang, Lizheng; Cheung, Jason Tak-Man; Pu, Fang; Li, Deyu; Zhang, Ming; Fan, Yubo (2011). "Why Do Woodpecker's Resist Head Impact Energy: A Biomechanical Investigation". PLOS One. 6 (10): e26490. doi:10.1371/journal.pone.0026490. PMC 3202538. PMID 22046293.
- Zimmer Biomet, Zimmer Inc. http://www.zimmerbiomet.com/medical-professionals/common/our-science/trabecular-metal-technology.html
| Look up trabecula in Wiktionary, the free dictionary. |