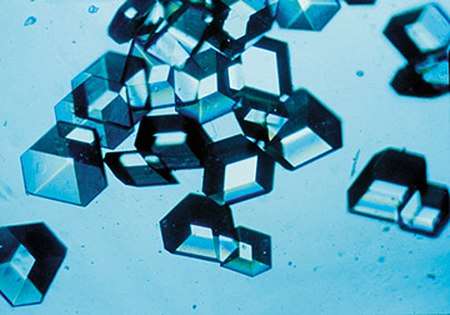படிக அமைப்பு
கனிமவியல் மற்றும் படிகவுருவியலில், படிக அமைப்பு என்பது ஓர் படிகத்தில் அணுக்கள் குறிப்பிட்ட அமைப்பில் உள்ளதைக் குறிப்பதாகும்.படிகம் (crystal) [1] என்பது அதனை உருவாக்கும் அணுக்கள், மூலக்கூறுகள், அயன்கள் என்பன ஒழுங்கமைவான முறையில், திரும்பத் திரும்ப வரும் வடிவொழுங்கில் ஓர் அணிக்கோவை அமைந்துள்ள ஒரு திண்மமாகும். அவ்வணிக்கோவையின் முனைகள் கொண்டு ஓர் பெட்டி அமைக்கப்படுமானால் அது ஓர் அலகுஅறையாக எடுத்துக் கொள்ளப்படுகிறது.இந்த அலகுஅறைகள் அணிக்கோவையை நிரப்புகின்றன. இந்த அலகுஅறையின் நீள,அகலங்கள் மற்றும் கோணங்கள் அணிக்கோவையின் வரையளவுகளாக குறிக்கப்படுகின்றன.படிகத்தின் சமச்சீர் பண்புகள் மூன்று அச்சுகளிலும் அமைகிறது. படிகத்தின் கட்டமைப்பும் சமச்சீர்மையும் பிளவு, இலத்திரன் பிணையமைப்பு மற்றும் ஒளி குறித்த பண்புகள் என அதன் பண்புகளை வரையறுக்கின்றன.
அலகுக் கூடு
படிகங்களில் அணுக்கள் அல்லது அயனிகள் ஒழுங்கான முப்பரிமான அமைப்பில் அமைந்துள்ளன. படிகத் திடப்பொருள் அல்லது படிகத்தில் உள்ள மிகச்சிறிய மீண்டும் மீண்டும் தோன்றக் கூடிய முப்பரிமாண வடிவமைப்பு அலகுக் கூடு எனப்படும். அலகுக் கூடு என்பது படிகத் திடப் பொருளின் எளிமையான அடிப்படைப் பகுதியாகும். அலகுக் கூட்டினை அறிவதன் மூலம் படிகத்தின் அமைப்பையும் அதில் அணுக்கள் அமைந்திருக்கும் விதத்தையும் அறியலாம். ஓர் அலகுக் கூடு அதன் அணிக்கோவை அளவுகளால் வருணிக்கப்படும், இவை அதன் கன நீளங்கள் (நீளம், அகலம், உயரம்) மற்றும் அவற்றிற்கு இடையிலான கோணங்கள் ஆகும். அலகுக் கூட்டில் அணுக்களின் இடங்கள் ஒரு அணிக்கோவை புள்ளியிலிருந்து அவ்வணுவின் தொலைவுகளால் (xi , yi , zi) தரப்படும்.
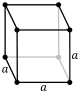
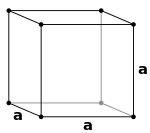 சாதரண கனசதுரம் (P)
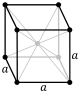
சாதரண கனசதுரம் (P)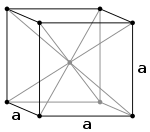 பொருள்மைய கனசதுரம் (I)
பொருள்மைய கனசதுரம் (I)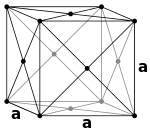 முகமைய கனசதுரம் (F)
முகமைய கனசதுரம் (F)
மில்லர் சுட்டெண்கள்
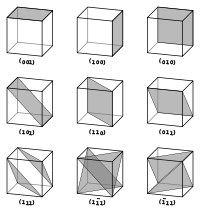
ஒரு படிக அணிக்கோவையில் உள்ள திசையன்களையும் அணுத்தளங்களையும் (ℓmn) என்ற மூவெண் மில்லர் சுட்டெண் குறியீட்டால் விவரிக்கலாம். இந்த ℓ, m மற்றும் n என்ற திசைச் சுட்டெண்கள் ஒன்றுக்கொன்று 90° விலகியிருக்கும், எனவே அவை செங்குத்தானவைகள் ஆகும்.
வரையறைப்படி, (ℓmn) என்பது அலகுக்கூட்டின் ஆய அச்சுகளில் a1/ℓ, a2/m மற்றும் a3/n என்ற மூன்று புள்ளிகளிலோ, அல்லது அவற்றின் பிற பன்மடிகளிலோ, வெட்டும் ஒரு தளத்தைக் குறிக்கும். அதாவது, மில்லர் சுட்டெண்கள் ஒரு அலகுக்கூட்டோடு ஒரு தளத்தின் வெட்டுப்புள்ளிகளின் எதிர்விகிதச்சமன்களாகும். ஒன்று அல்லது அதற்கு மேற்பட்ட சுட்டெண்கள் சுழியம் என்றால் அத்தளம் அந்தந்த அச்சுகளை வெட்டவில்லை என்பது பொருள் (அதாவது முடிவிலியில் வெட்டு, அல்லது அத்தளம் அவ்வச்சிற்கு இணை ஆகும்). இணைத் தளங்களின் மில்லர் சுட்டெண்கள் சமமாகவே இருக்கும். ஏதேனும் ஒரு ஆய அச்சினை உள்ளடக்கிய ஒரு தளத்தின் மில்லர் சுட்டெண்களைக் கணக்கிட அத்தளத்திற்கு இணையான வேறொரு தளம் கொள்ளப்படும். ஒரு தளத்தின் மில்லர் சுட்டெண்கள் தமக்குள் பொதுக்காரணின் இல்லா முழுஎண்கள் ஆகும். எதிர்ம சுட்டெண்கள் அவற்றின் மீது இடப்படும் கோட்டினால் குறிக்கப்படும், (123) இவ்வாறு. ஒரு செங்குத்து ஆய திட்டத்தில், ஒரு தளத்தின் மில்லர் சுட்டெண்கள் அத்தளத்தின் செங்குத்து திசையனின் கார்ட்டீசியன் கூறுகள் ஆகும்.
(ℓmn) சுட்டெண்களால் குறிக்கப்படும் இணை அணிக்கோவை தளங்கள் இரண்டிற்கு இடையிலான குறைவான செங்குத்து தொலைவு d பின்வரும் வாய்ப்பாட்டால் தரப்படும்:
ஏழு அணிக்கோவை அமைப்பு
அணிக்கோவைகளின் அச்சு அமைப்பினைக்கொண்டு படிக அமைப்புகள் ஏழு குழுக்களாக பிரிக்கப்படுகின்றன. ஒவ்வொரு அணிக்கோவையும் மூன்று அச்சுகளிலும் ஓர் குறிப்பிட்ட அமைப்பைக் கொண்டிருக்கும்.
| ஏழு அணிக்கோவை அமைப்புகள் (குறைந்ததிலிருந்து கூடுதல் சமச்சீர்மை கொண்டது வரை) |
14 ப்ராவை அணிக்கோவைகள் | எடுத்துக்காட்டுகள் | ||||||
| 1. முச்சாய்வு (triclinic)(none) |
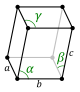 | |||||||
| 2. ஒருசாய்வு (monoclinic) (1 diad) |
simple | base-centered | ||||||
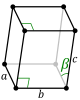 |
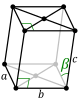 | |||||||
| 3. சமமில்லா முச்செங்குத்து <orthorhombic) (3 perpendicular diads) |
simple | base-centered | body-centered | face-centered | ||||
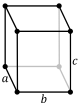 |
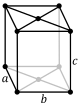 |
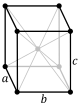 |
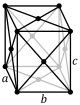 | |||||
| 4. சமபக்க முச்சாய்வகம் (rhombohedral) (1 triad) |
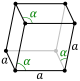 | |||||||
| 5. சதுரப்பட்டகம் (tetragonal) (1 tetrad) |
simple | body-centered | ||||||
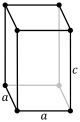 |
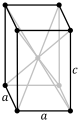 | |||||||
| 6. அறுகோணப்பட்டகம் (hexogonal) (1 hexad) |
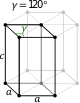 | |||||||
| 7. கனசதுரம் (4 triads) |
simple (SC) | body-centered (BCC) | face-centered (FCC) | |||||
 |
 |
 | ||||||