பித்தகோரசு பகாத்தனி

$4n+1$ என்ற வடிவில் அமையும் பகாத்தனிகள் பித்தகோரசு பகாத்தனிகள் அல்லது பித்தகோரசு பகாஎண்கள் (Pythagorean prime) என அழைக்கப்படுகின்றன.

எடுத்துக்காட்டுகள்

5, 13, 17 ஆகிய மூன்று பகாத்தனிகளும் பித்தகோரசு பகாக்தனிகள்.

இவை $5=4\times 1+1$ வடிவில் அமைவதைக் காணலாம்:

5=4\times 1+1

13=4\times 3+1

17=4\times 4+1

மேலும் பித்தகோரசு பகாத்தனிகள், ஒற்றைப் பகாத்தனிகளாக இருப்பதையும் இரு வர்க்கஎண்களின் கூடுதலாக இருப்பதையும் காணலாம்:

5=2^{2}+1^{2}

13=3^{2}+2^{2}

17=4^{2}+1^{2}

இரு முழுஎண் தாங்குபக்கங்களைக் கொண்ட இரு வெவ்வேறு செங்கோண முக்கோணங்களின் செம்பக்கங்களாகப் பித்தாகரசு பகாத்தனி p ம், அதன் வர்க்கமூலமும் ( ${\sqrt {p}}$ ) அமைகின்றன.

படம் 1:பித்தாகரசு பகாத்தனி 5ம் அதன் வர்க்கமூலமும் முழுஎண் தாங்குபக்கங்களைக் கொண்ட இரு செங்கோண முக்கோணங்களின் செம்பக்கங்களாக இருப்பதைக் காணலாம்.

எடுத்துக்காட்டு

5 ஒரு பித்தாகரசு பகாத்தனி; அதன் வர்க்கமூலம்: ${\sqrt {5}}$

1, 2 தாங்கு பக்கநீளங்கள் கொண்ட செங்கோண முக்கோணத்தின் செம்பக்கமாக ${\sqrt {5}}$ ம், 3, 4 தாங்கு பக்கநீளங்கள் கொண்ட செங்கோண முக்கோணத்தின் செம்பக்கமாக 5ம் இருப்பதை மேலேயுள்ள படத்தில் காணலாம்.

மதிப்புகளும் அடர்த்தியும்

சில பித்தகோரசு பகாத்தனிகள்:

5, 13, 17, 29, 37, 41, 53, 61, 73, 89, 97, 101, 109, 113, … (OEIS-இல் வரிசை A002144)

.

திரிசிலேயின் (Dirichlet) கூட்டுத் தொடர்களுக்கானத் தேற்றத்தின்படி, பித்தகோரசு பகாத்தனிகளின் தொடர்முறை முடிவில்லாதது ஆகும்.

ஒவ்வொரு எண் nக்கும், n வரையிலான பித்தகோரசு பகாத்தனிகளின் எண்ணிக்கையும், அவற்றைத் தவிர மீதமுள்ள பகாத்தனிகளின் எண்ணிக்கையும் கிட்டத்தட்ட சமமாக இருக்கும். எனினும் n வரையிலான பித்தகோரசு பகாத்தனிகளின் எண்ணிக்கையானது, அவற்றைத் தவிர மீதமுள்ள பிற பகாத்தனிகளின் எண்ணிக்கையைக் காட்டிலும் பெரும்பாலும் கொஞ்சம் சிறியதாகவே இருக்கும்.[1]

எடுத்துக்காட்டாக, 600000 வரையிலான n இன் மதிப்புகளில், n = 26861, 26862 என்ற இரண்டு மதிப்புகளுக்கு மட்டுமே, அந்த எண்கள் வரையிலான பித்தாகரசு பகாத்தனிகளின் எண்ணிக்கையானது, மீதமுள்ள பித்தாகரசு பகாத்தனிகளல்லாத ஒற்றைப் பகாத்தனிகளின் எண்ணிக்கையைக் காட்டிலும் அதிகம்.[2]

இருவர்க்கங்களின் கூடுதலாக அமைதல்

இரு வர்க்கங்களின் கூடுதலாக அமையும் ஒற்றை எண்கள் அனைத்தும் மாடுலோ 4 ஐப்பொறுத்து எண் 1 க்குச் சமானமாக இருக்கும். அதாவது, $4n+1$ என்ற வடிவில் அமையும். ஆனால் மாடுலோ 4 ஐப்பொறுத்து எண் 1 க்குச் சமானமானதாக இருக்கும் ஒற்றை எண்கள் எல்லாம் இரு வர்க்கங்களின் கூடுதலாக அமைவதில்லை. எடுத்துக்காட்டாக,

21\equiv 1

(mod

4

). ஆனால் 21ஐ எந்த இரு வர்க்கங்களின் கூடுதலாகவும் எழுத முடிவதில்லை.

பெர்மாவின் தேற்றம் (இரு வர்க்கங்களின் கூடுதல்)

இரு வர்க்கங்களின் கூடுதல் குறித்த இரு வர்க்கங்களின் கூடுதல் மீதான பெர்மாவின் தேற்றத்தின் கூற்றின்படி:

எண் 2ம், மாடுலோ 4 ஐப்பொறுத்து எண் 1 க்குச் சமானமாக இருக்கும் ஒற்றைப் பகாத்தனிகள் மட்டுமே, இரு வர்க்கங்களின் கூடுதலாக எழுதக் கூடிய பகாத்தனிகள் ஆகும்.[3] மேலும், அவற்றை இரு வர்க்கங்களின் கூடுதலாக எழுதும் முறையும் தனித்துவமானதாகும்.[4]

எனவே, மாடுலோ 4 ஐப்பொறுத்து எண் 1 க்குச் சமான (

4n+1

என்ற வடிவில் அமையும்) ஒற்றைப்பகாத்தனிகள் பித்தாகரசு பகாத்தனிகள் என்பதால் பெர்மாவின் தேற்றப்படி, பித்தாகரசு பகாத்தனிகளை இரு வர்க்கங்களின் கூடுதலாக தனித்துவமாக எழுதுவது சாத்தியமாகிறது.

வடிவவியல் விளக்கம்

இவ்வாறு பித்தகோரசு பகாத்தனியை இரு வர்க்கங்களின் கூடுதலாக எழுதும் முறையைப் பித்தகோரசு தேற்றத்தைப் பயன்படுத்தி வடிவவியலாக விளக்கலாம்:

p ஒரு பித்தகோரசு பகாத்தனி எனில்,

{\sqrt {p}}

ஐச் செம்பக்கமாகவும் இரு முழுஎண் தாங்கு பக்கங்களையும் கொண்ட ஒரு செங்கோண முக்கோணம் இருக்கும்.

(அதாவது செங்கோண முக்கோணத்தில் பித்தகோரசு தேற்ற முடிவின் படி p பகாத்தனியை (செம்பக்கத்தின் வர்க்கம்) இரு வர்க்கங்களின் கூடுதல் (தாங்கு பக்கங்களின் வர்க்கங்களின் கூடுதலாக) எழுதலாம்.)

எடுத்துக்காட்டு:

13 ஓர் ஒற்றைப் பகாத்தனி. இதனை இரு வர்க்கங்களின் கூடுதலாக எழுத,

{\sqrt {1}}3=4+9=2^{2}+3^{2}.

எனவே பித்தகோரசு தேற்றப்படி, 2, 3, ${\sqrt {1}}3$ (செம்பக்கம்) மூன்றும் ஒரு செங்கோண முக்கோணத்தின் பக்கங்களாக உள்ளது.

பித்தாகரசு பகாத்தனிகளுக்கு (p), அவற்றின் வர்க்கமூலங்களைச் செம்பக்கங்களாகக் கொண்ட செங்கோண முக்கோணங்கள் மட்டுமல்லாது, அவற்றையே செம்பக்கமாகவும், இரு முழுஎண் தாங்கு பக்கங்களையும் கொண்ட செங்கோண முக்கோணங்களும் உண்டு.

விளக்கம் (படம் 1)

p என்ற பித்தாகரசு பகாத்தனிக்குரிய செங்கோண முக்கோணத்தின் பக்கங்கள் ${\sqrt {p}},$ (செம்பக்கம்) x , y எனில் பித்தகோரசு தேற்றப்படி,

(x^{2}+y^{2})^{2}=p^{2}\quad (*)

இப்போது, x² − y², 2xy இரண்டையும் தாங்கு பக்கங்களாகக் கொண்ட செங்கோண முக்கோணத்தின் செம்பக்கம் p ஆக இருக்கும் என்பதைக் காணலாம்[5]:

(x^{2}-y^{2})^{2}+(2xy)2

= $(x^{2}+y^{2})^{2}$ = $p^{2}$ (* ஐப் பயன்படுத்த)

இருபடிய எச்சங்கள்

இருபடி நேர்எதிர்மை விதிப்படி, p , q இரு வெவ்வேறான ஒற்றைப் பகாத்தனிகள்; மேலும் இரண்டில் ஒன்றாவது பித்தகோரசு பகாத்தனி எனில்:

q ஒரு இருபடிய எச்சமாக (மாடுலோ p) இருந்தால், இருந்தால் மட்டுமே, p ஒரு இருபடிய எச்சமாக (மாடுலோ q) இருக்கும்.

மாறாக, p , q இரண்டுமே பித்தகோரசு பகாத்தனிகள் இல்லையெனில்:

q இருபடிய எச்சமாக (மாடுலோ p) இல்லாமல் இருந்தால், இருந்தால் மட்டுமே, p இருபடிய எச்சமாக (மாடுலோ q) இருக்கும்.[6]

p ஒரு பித்தகோரசு பகாத்தனி எனில்:

Z/p என்ற முடிவுறு களத்தில், சமன்பாடு x² = −1 சமன்பாட்டிற்கு இருதீர்வுகள் உள்ளன. −1 இருபடிய எச்சமாக (மாடுலோ p) இருப்பதால் இத் தீர்வுகள் கிடைக்கின்றன.

மாறாக, p ஒரு ஒற்றைப் பகாத்தனி ஆனால் பித்தகோரசு பகாத்தனி இல்லையெனில்:

Z/p என்ற முடிவுறு களத்தில், சமன்பாடு x² = −1 சமன்பாட்டிற்குத் தீர்வுகள் இல்லை.[7]

பாலே வரைபடம்

13 உச்சிகள் கொண்ட பாலே வரைபடம்

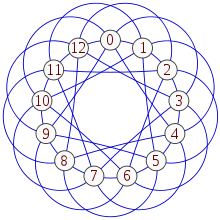
ஒவ்வொரு பித்தகோரசு பகாத்தனிக்கும் பாலே வரைபடம் உள்ளது. p ஒரு பித்தகோரசு பகாத்தனி எனில் மாடுலோ p எண்களைக் குறிக்கும் பாலே வரைபடமானது p உச்சிகளைக் கொண்டிருக்கும். இரு மாடுலோ p எண்களின் வித்தியாசம் ஒரு இருபடிய எச்சமாக இருந்தால், இருந்தால் மட்டுமே, அந்த இரு எண்களும் பாலே வரைபடத்தில் அடுத்தடுத்த உச்சிகளாக இருக்க முடியும்.[8]

மேற்கோள்கள்

Rubinstein, Michael; Sarnak, Peter (1994), "Chebyshev's bias", Experimental Mathematics 3 (3): 173–197, doi:10.1080/10586458.1994.10504289.
Andrew Granville; Martin, Greg (January 2006). "Prime Number Races". American Mathematical Monthly 113 (1): 1--33. doi:10.2307/27641834. http://www.dms.umontreal.ca/%7Eandrew/PDF/PrimeRace.pdf.
Ian Stewart (mathematician) (2008), Why Beauty is Truth: A History of Symmetry, Basic Books, p. 264, பன்னாட்டுத் தரப்புத்தக எண்:9780465082377, http://books.google.com/books?id=6akF1v7Ds3MC&pg=PA264.
William J. LeVeque (1996), Fundamentals of Number Theory, Dover, p. 183, பன்னாட்டுத் தரப்புத்தக எண்:9780486689067, http://books.google.com/books?id=F6aJtNcwyw8C&pg=PA183.
John Stillwell (2003), Elements of Number Theory, Undergraduate Texts in Mathematics, Springer, p. 112, பன்னாட்டுத் தரப்புத்தக எண்:9780387955872, http://books.google.com/books?id=LiAlZO2ntKAC&pg=PA112
LeVeque (1996), p. 103.
LeVeque (1996), p. 100.
Fan Chung (1997), Spectral Graph Theory, CBMS Regional Conference Series, 92, American Mathematical Society, pp. 97–98, பன்னாட்டுத் தரப்புத்தக எண்:9780821889367, http://books.google.com/books?id=YUc38_MCuhAC&pg=PA97.

வெளி இணைப்புகள்

Eaves, Laurence. "Pythagorean Primes: including 5, 13 and 137". Numberphile. Brady Haran.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Rubinstein, Michael; Sarnak, Peter (1994), "Chebyshev's bias", Experimental Mathematics 3 (3): 173–197, doi:10.1080/10586458.1994.10504289.

[Granville_Martin_MAA-2] Andrew Granville; Martin, Greg (January 2006). "Prime Number Races". American Mathematical Monthly 113 (1): 1--33. doi:10.2307/27641834. http://www.dms.umontreal.ca/%7Eandrew/PDF/PrimeRace.pdf.

[3] Ian Stewart (mathematician) (2008), Why Beauty is Truth: A History of Symmetry, Basic Books, p. 264, பன்னாட்டுத் தரப்புத்தக எண்:9780465082377, http://books.google.com/books?id=6akF1v7Ds3MC&pg=PA264.

[4] William J. LeVeque (1996), Fundamentals of Number Theory, Dover, p. 183, பன்னாட்டுத் தரப்புத்தக எண்:9780486689067, http://books.google.com/books?id=F6aJtNcwyw8C&pg=PA183.

[5] John Stillwell (2003), Elements of Number Theory, Undergraduate Texts in Mathematics, Springer, p. 112, பன்னாட்டுத் தரப்புத்தக எண்:9780387955872, http://books.google.com/books?id=LiAlZO2ntKAC&pg=PA112

[6] LeVeque (1996), p. 103.

[7] LeVeque (1996), p. 100.

[8] Fan Chung (1997), Spectral Graph Theory, CBMS Regional Conference Series, 92, American Mathematical Society, pp. 97–98, பன்னாட்டுத் தரப்புத்தக எண்:9780821889367, http://books.google.com/books?id=YUc38_MCuhAC&pg=PA97.