বহুভাঁজ

গণিতে বহুভাঁজ হল এমন এক টপোলজিকাল স্থান যা স্থানীয়ভাবে প্রতিটি বিন্দুর নিকটে ইউক্লিডীয় স্থানের সমরূপ হবে। আরও সঠিকভাবে বলা যায়, একটি n-মাত্রিক বহুভাঁজের প্রতিটি বিন্দুর একটি সমীপবর্তিতা বিদ্যমান যা n মাত্রার ইউক্লিডীয় স্থানে হোমিওমর্ফিক। আরও নিখুঁত পরিভাষায়, একটি বহুভাঁজ বলতে n-বহুভাঁজকে বোঝানো হয়।

প্রকৃত প্রক্ষেপণ সমতল হল একটি দ্বিমাত্রিক বহুভাঁজ যা স্বতঃপ্রতিচ্ছেদ ছাড়া ত্রিমাত্রিক ভাবে বোধগম্য নয়। একে এখানে বালকের পৃষ্ঠের মাধ্যমে দেখানো হয়েছে।

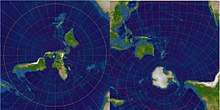
পৃথিবী পৃষ্ঠের প্রতিটি বিন্দুর অন্তর্ভুক্তির জন্য (ন্যূনতম) দুইটি বর্ণনা চিত্র বা মানচিত্রের প্রয়োজন। এখানে পৃথিবী পৃষ্ঠকে উত্তর ও দক্ষিণ মেরু এ দুটি পরিমণ্ডলে বিভাজিত করা হয়েছে।

তথ্যসূত্র

Freedman, Michael H., and Quinn, Frank (1990) Topology of 4-Manifolds. Princeton University Press. আইএসবিএন ০-৬৯১-০৮৫৭৭-৩.
Guillemin, Victor and Pollack, Alan (1974) Differential Topology. Prentice-Hall. আইএসবিএন ০-১৩-২১২৬০৫-২. Advanced undergraduate / first-year graduate text inspired by Milnor.
Hempel, John (1976) 3-Manifolds. Princeton University Press. আইএসবিএন ০-৮২১৮-৩৬৯৫-১.
Hirsch, Morris, (1997) Differential Topology. Springer Verlag. আইএসবিএন ০-৩৮৭-৯০১৪৮-৫. The most complete account, with historical insights and excellent, but difficult, problems. The standard reference for those wishing to have a deep understanding of the subject.
Kirby, Robion C. and Siebenmann, Laurence C. (1977) Foundational Essays on Topological Manifolds. Smoothings, and Triangulations. Princeton University Press. আইএসবিএন ০-৬৯১-০৮১৯০-৫. A detailed study of the category of topological manifolds.
Lee, John M. (2000) Introduction to Topological Manifolds. Springer-Verlag. আইএসবিএন ০-৩৮৭-৯৮৭৫৯-২. Detailed and comprehensive first-year graduate text.
Lee, John M. (2003) Introduction to Smooth Manifolds. Springer-Verlag. আইএসবিএন ০-৩৮৭-৯৫৪৯৫-৩. Detailed and comprehensive first-year graduate text; sequel to Introduction to Topological Manifolds.
Massey, William S. (1977) Algebraic Topology: An Introduction. Springer-Verlag. আইএসবিএন ০-৩৮৭-৯০২৭১-৬.
Milnor, John (1997) Topology from the Differentiable Viewpoint. Princeton University Press. আইএসবিএন ০-৬৯১-০৪৮৩৩-৯. Classic brief introduction to differential topology.
Munkres, James R. (1991) Analysis on Manifolds. Addison-Wesley (reprinted by Westview Press) আইএসবিএন ০-২০১-৫১০৩৫-৯. Undergraduate text treating manifolds in Rⁿ.
Munkres, James R. (2000) Topology. Prentice Hall. আইএসবিএন ০-১৩-১৮১৬২৯-২.
Neuwirth, L. P., ed. (1975) Knots, Groups, and 3-Manifolds. Papers Dedicated to the Memory of R. H. Fox. Princeton University Press. আইএসবিএন ৯৭৮-০-৬৯১-০৮১৭০-০.
Riemann, Bernhard, Gesammelte mathematische Werke und wissenschaftlicher Nachlass, Sändig Reprint. আইএসবিএন ৩-২৫৩-০৩০৫৯-৮.
- Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse. The 1851 doctoral thesis in which "manifold" (Mannigfaltigkeit) first appears.
- Ueber die Hypothesen, welche der Geometrie zu Grunde liegen. The 1854 Göttingen inaugural lecture (Habilitationsschrift).
Spivak, Michael (1965) Calculus on Manifolds: A Modern Approach to Classical Theorems of Advanced Calculus. W.A. Benjamin Inc. (reprinted by Addison-Wesley and Westview Press). আইএসবিএন ০-৮০৫৩-৯০২১-৯. Famously terse advanced undergraduate / first-year graduate text.
Spivak, Michael (1999) A Comprehensive Introduction to Differential Geometry (3rd edition) Publish or Perish Inc. Encyclopedic five-volume series presenting a systematic treatment of the theory of manifolds, Riemannian geometry, classical differential geometry, and numerous other topics at the first- and second-year graduate levels.
Tu, Loring W. (২০১১)। An Introduction to Manifolds (2nd সংস্করণ)। New York: Springer। আইএসবিএন 978-1-4419-7399-3।. Concise first-year graduate text.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.