অতিবেগুনী বিপর্যয়

অতিবেগুনী বিপর্যয় বা আলট্রাভায়োলেট ক্যাটাস্ট্রফি (যা র‍্যালে-জিন্স ক্যাটাস্ট্রফি নামেও পরিচিত) হল উনিশ শতকের শেষ দিকে বা বিশ শতকের প্রথম দিককার ক্ল্যাসিকাল পদার্থবিজ্ঞানের একটি ঘটনা। ক্ল্যাসিকাল পদার্থবিজ্ঞান মতে আদর্শ কৃষ্ণবস্তু তাপীয় সাম্যাবস্থায় থেকে সকল কম্পাঙ্কের বিকিরণ ঘটায় এবং কম্পাঙ্ক বৃদ্ধির সাথে সাথে শক্তির বিকিরণ বৃদ্ধি পায়। মোট বিকিরিত শক্তি পরিমাপ করে দেখানো যায় যে কৃষ্ণবস্তু অসীম পরিমাণ শক্তির নির্গমন ঘটাবে যা কিনা শক্তির নিত্যতার নীতির সুস্পষ্ট লঙ্ঘন। তখনই এ সম্পর্কিত নতুন কোনো তত্ত্বের প্রয়োজনীয়তা অনুভূত হয়।

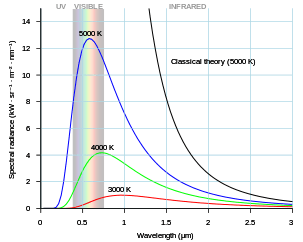
র‍্যালে জিন্স সূত্রে ক্ষুদ্র তরঙ্গের ক্ষেত্রে আদর্শ কৃষ্ণবস্তু থেকে বিকিরিত শক্তির অতিবেগুনী বিপর্যয়। ক্ষুদ্র তরঙ্গদৈর্ঘ্যের এই ভুল হল কালো বক্ররেখা (র‍্যালে-জিন্স সূত্রমতে প্রাপ্ত) এবং নীল বক্ররেখাটি হল (প্লাঙ্কের সূত্রমতে প্রাপ্ত)।

১৯১১ সালে পল হেরেনফেস্ট সর্বপ্রথম "আলট্রাভায়োলেট ক্যাটাস্ট্রফি" শব্দদ্বয় ব্যবহার করেন, তবে মূলত ১৯০০ সালের দিকে র‍্যালে-জিনস সূত্র আবিষ্কারের সময়ই এ ধারণার উৎপত্তি হয়। ১০৫ গিগাহার্জের চেয়ে কম বিকিরিত কম্পাঙ্কের মধ্যের সবধরনের পরীক্ষামূলক ফলাফলের ব্যাখ্যা এ সূত্র নিখুঁতভাবে দিতে পারলেও এ সীমার বাইরের পরীক্ষামূলক ব্যাখ্যার ফলাফল দিতে এ সূত্র ব্যর্থ হয়। তখন তাত্ত্বিক আর পরীক্ষামূলক ফলাফল ভিন্ন হয়ে পড়ে। এই ভিন্নতার সৃষ্টি তড়িতচুম্বকীয় বর্ণালীর অতিবেগুনী রশ্মির সীমা থেকে শুরু হওয়ায় এ ঘটনাকে "অতিবেগুনী বিপর্যয়" বলে অভিহিত করা হয়।[1] এ শব্দগুচ্ছের প্রথম ব্যবহারের পর প্রায় একই ধরনের আরেক ঘটনার ক্ষেত্রেও এই শব্দগুচ্ছ ব্যবহার করা হয়, যেমন কোয়ান্টাম ইলেকট্রোডায়নামিক্সে বা অতিবেগুনী ডাইভারজেন্সে।

সমস্যা

ক্ল্যাসিকাল স্ট্যাটিসটিকাল মেকানিক্সের সমবিভাজন নীতি থেকেই অতিবেগুনী বিপর্যয়ের সূত্রপাত। এ নীতিমতে সাম্যাবস্থায় সকল ছন্দিত স্পন্দকের প্রত্যেক স্বাধীনতার মাত্রার গড় শক্তি হবে ।

উদাহরণস্বরূপ, ম্যাসনের আ হিস্ট্রি অব দ্য সায়েন্সেস থেকে,[2] দেখা যায় একটি তারের অংশের বিভিন্ন কম্পন। প্রাকৃতিক স্পন্দক হিসেবে তারটি এর দৈর্ঘ্যের উপর ভিত্তি করে কম্পিত হবে। সনাতন পদার্থবিজ্ঞানে শক্তি-বিকিরক, প্রাকৃতিক স্পন্দক হিসেবে কাজ করে। এবং যেহেতু স্বাধীনতার মাত্রাপিছু একই শক্তি, প্রাকৃতিক স্পন্দকের অধিকাংশ শক্তি ক্ষুদ্র তরঙ্গদৈর্ঘ্য এবং উচ্চ কম্পাঙ্কবিশিষ্ট হবে।

ক্ল্যাসিকাল ইলেকট্রোম্যাগনেটিজম অনুযায়ী একটি তিন-মাত্রার গহ্বরের প্রতি একক কম্পাঙ্কে মোট তড়িৎচুম্বকীয় মাত্রা, কম্পাঙ্কের বর্গের সমাণুপাতিক হবে। অতএব প্রতি একক কম্পাঙ্কে বিকিরিত শক্তির র‍্যালে-জিন্স সূত্র মেনে চলা উচিত এবং কম্পাঙ্কের বর্গের সমানুপাতিক হওয়া উচিত। অতএব একটি নির্দিষ্ট কম্পাঙ্কে ক্ষমতা এবং মোট বিকিরিত ক্ষমতা অসীম হবে, যখন কম্পাঙ্ক অসীমের দিকে ধাবিত হবে। এটা হতে পারে না কারণ একটি গহ্বরের মোট বিকিরিত শক্তি কোনোক্রমেই অসীম হতে পারে না; যে বিষয়ে স্বাধীনভাবে আলবার্ট আইনস্টাইন, লর্ড র‍্যালে এবং স্যার জেমস জিনস ১৯০৫ সালে উপনীত হন।

সমাধান

ম্যাক্স প্লাঙ্ক কিছু অদ্ভূত পরিবর্তনের মাধ্যমে বর্ণালীর বণ্টন ফাংশনকে সঠিক করে তোলেন। প্লাঙ্ক পরবর্তীতে একে "ভাগ্যক্রমে মিলে যাওয়া অনুমান" (লাকি গেজওয়ার্ক) বলে অভিহিত করেন। এ পরিবর্তন থেকে পরবর্তীতে ধারণা করা হয় যে তড়িৎচুম্বকীয় বিকিরণ কেবলমাত্র কিছু প্যাকেটের আকারেই বিকিরিত বা শোষিত হতে পারে। শক্তির এই প্যাকেটকে বলা হয় কোয়ান্টাম (বহুবচনে কোয়ান্টা)। এ লাতিন শব্দের অর্থ "কতটুকু"। শক্তির কোয়ান্টা: , যেখানে h হল প্লাঙ্কের ধ্রুবক। প্লাঙ্কের এ পরিবর্তন বর্ণালি বণ্টন ফাংশনকে পরিবর্তিত করে সঠিকাবস্থায় নিয়ে আসে: । আইনস্টাইন পরবর্তীতে এ সমস্যার সমাধান করেন এই ধারণার ভিত্তিতে যে প্লাঙ্কের কোয়ান্টা বস্তুত বাস্তব কণা-যাকে বর্তমানে আমরা ফোটন বলে থাকি। এটা কোনো গাণিতিক কল্পকাহিনি নয়। তিনি বোল্টজম্যানের মত স্ট্যাটিসটিকাল মেকানিক্সকে পরিবর্ধন করেন এবং সেখানে ফোটনকে অন্তর্ভুক্ত করেন। আইনস্টাইনের ফোটনের শক্তি এর কম্পাঙ্কের সমানুপাতিক এবং স্টোকসের অপ্রকাশিত সূত্র ও ফটোইলেকট্রিক এফেক্টকেও ব্যাখ্যা করে।[3]

ঐতিহাসিক ভুল

পদার্থবিজ্ঞানের অনেক বিখ্যাত ইতিহাস এবং বেশকিছু পদার্থবিজ্ঞানবিষয়ক বইতেও অতিবেগুনী বিপর্যয় সম্পর্কে ভুল ইতিহাস জানানো হয়। বলা হয় প্লাঙ্কই সর্বপ্রথম "ক্যাটাসট্রোফি" শব্দগুচ্ছ ব্যবহার করে। কিন্তু প্রকৃতপক্ষে প্লাঙ্ক কখনই এ বিষয়ে ভাবেননি কারণ তিনি সমবিভাজন নীতিকে মৌলিক বলে মানতেন না। "কোয়ান্টা"র আবির্ভাগের কারণ ছিল সম্পূর্ণ ভিন্ন। তবে প্লাঙ্কের প্রস্তাব এ সমস্যার একটি সমাধান করে দেয় বটে।[4] ধীরে ধীরে ঐতিহাসিকেরা সত্য ঘটনা জানতে পারলেও অনেক ঐতিহাসিক ভুল ইতিহাসকেই সমর্থন করে, যার আংশিক কারণ সম্ভবত কোয়ান্টাম উদঘাটনের প্রকৃত কারণ কিছুটা জটিল এবং সহজে উপস্থাপন কষ্টসাধ্য।[5]

আরো দেখুন
  • উইন সন্নিকর্ষতা
  • শূন্যতা বিপর্যয়

তথ্যসূত্র
  1. McQuarrie, Donald A.; Simon, John D. (১৯৯৭)। Physical chemistry: a molecular approach (rev. সংস্করণ)। Sausalito, Calif.: Univ. Science Books। আইএসবিএন 978-0-935702-99-6।
  2. Mason, Stephen F. (১৯৬২)। A History of the Sciences। Collier Books। পৃষ্ঠা 550।
  3. Stone, A. Douglas (২০১৩)। Einstein and the Quantum। Princeton University Press।
  4. Kragh, Helge (ডিসেম্বর ২০০০)। "Max Planck: The reluctant revolutionary"। Physics World।
  5. Kuhn, Thomas (১৯৭৮)। Black-Body Theory and the Quantum Discontinuity, 1894-1912। Clarendon Press, Oxford। আইএসবিএন 0-226-45800-8।
    Galison, Peter (১৯৮১)। "Kuhn and the Quantum Controversy"। British Journal for the Philosophy of Science। 32 (1): 71–85। doi:10.1093/bjps/32.1.71।

আরো পড়ুন
  • Kroemer, Herbert; Kittel, Charles (১৯৮০)। "Chapter 4"। Thermal Physics (2 সংস্করণ)। W. H. Freeman Company। আইএসবিএন 0-7167-1088-9।
  • Cohen-Tannoudji, Claude; Diu, Bernard; Laloë; Franck (১৯৭৭)। Quantum Mechanics: Volume One। Hermann, Paris। পৃষ্ঠা 624–626। আইএসবিএন 0-471-16433-X।
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.