e (গাণিতিক ধ্রুবক)
e হলো প্রাকৃতিক লগারিদমের ভিত্তি। এটি একটি বাস্তব সংখ্যা যার সংখ্যাগত মান হলো ২.৭১৮ ২৮১ ৮২৮ ৪...[1]
| গাণিতিক ধ্রুবক e |
|---|
| নিবন্ধের ধারাবাহিকের অংশ |
 |
| Properties |
|
| Applications |
|
| Defining e |
|
| ব্যক্তি |
| Related topics |
|
সংজ্ঞা
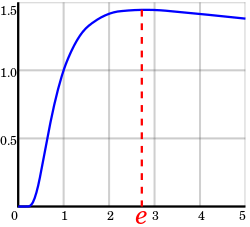
অর্থাৎ e হলো প্রদত্ত রাশিটির সীমা, যখন n এর মান অসীম পর্যন্ত বৃদ্ধি পায়। অন্য কথায়, n এর মান যত বৃদ্ধি পায়, রাশিটির মান তত e এর কাছাকাছি যেতে থাকে।
মান নির্ণয়
১ + ১/১! + ১/২! + ১/৩! + ১/৪! + ... অসীম ধারাটির সমষ্টি e এর সমান।[2]
প্রমাণটাও সহজ, প্যাসক্যালের বাইনোমিয়াল সূত্র বলে,
সুতরাং, যখন , তখন,
যার সীমা হলো e (কারণ n এর মান যত বৃদ্ধি পায়, এর মান তত শুন্যের দিকে কমতে থাকে)।
সূচক ফাংশন
রাশিটিকে x এর ফাংশন হিসেবে ধরে একে সূচক ফাংশন বলা হয়। একে ও লেখা হয়।
ফাংশনটিকে একটি অসীম ধারা হিসেবে লেখা যায় (এই ধারাটি কোন নির্দিষ্ট x এর জন্য ফাংশনটির মান নির্ণয়েও ব্যবহৃত হয়),
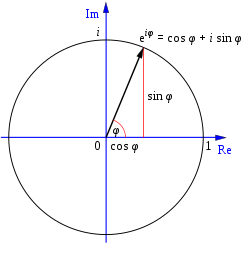
অয়লারের অভেদ
সমীকরণটি e কে ১, π এবং i এর মতন গুরুত্বপূর্ণ সংখ্যার সাথে সম্পর্কিত করে। ১৭৩৭ সালে অয়লার[3] দেখান যে, e একটি অমূলদ সংখ্যা। ১৮৭৩ সালে হেরমিট প্রমাণ করেন যে, e একটি তুরীয় সংখ্যা(π পাই এর মত)
তথ্যসূত্র
- Oxford English Dictionary, 2nd ed.: natural logarithm
- Encyclopedic Dictionary of Mathematics 142.D
- Sondow, Jonathan। "e"। Wolfram Mathworld। Wolfram Research। সংগ্রহের তারিখ ১০ মে ২০১১।
বহিঃসংযোগ
| উইকিমিডিয়া কমন্সে E (গাণিতিক ধ্রুবক) সংক্রান্ত মিডিয়া রয়েছে। |