பிரகார்டு புள்ளி

முக்கோணம் ABC இன் பக்கங்கள் a, b, c. மேலும் அதன் உச்சிகள் A, B, C மூன்றும் எதிர் கடிகாரதிசையில் பெயரிடப்பட்டுள்ளது எனில்:

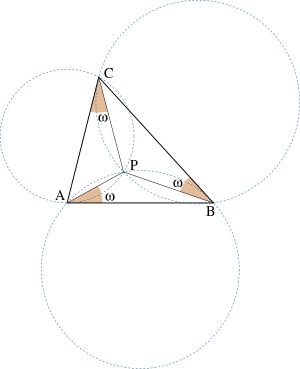
• கோட்டுத்துண்டுகள் AP, BP, CP மூன்றும் முறையே பக்கங்கள் c, a, b உடன் உண்டாக்கும் மூன்று கோணங்களும் சமவளவாக அமையக்கூடியவாறு, P என்று ஒரேயொரு புள்ளி மட்டுமே இருக்க முடியும்.

${\displaystyle \angle PAB=\angle PBC=\angle PCA=\omega .\,}$

புள்ளி P ஆனது ABC முக்கோணத்தின் முதல் பிரகார்டு புள்ளி எனவும் கோணம் ω , பிரகார்டு கோணம் எனவும் அழைக்கப்படுகிறது. பிரகார்டு கோணம் கீழுள்ள முடிவை நிறைவு செய்கிறது:

${\displaystyle \cot \omega =\cot \alpha +\cot \beta +\cot \gamma .\,}$

• கோட்டுத்துண்டுகள் AQ, BQ, CQ மூன்றும் முறையே பக்கங்கள் b, c, a உடன் உண்டாக்கும் மூன்று கோணங்களும் சமவளவாக அமையக்கூடியவாறு இந்த இரண்டாவது பிரகார்டு புள்ளி Q அமையும். அதாவது,

${\displaystyle \angle QCB=\angle QBA=\angle QAC}$

இம்மூன்று சமகோணங்களின் அளவும் ${\displaystyle \omega \,}$ ஆக இருக்கும்.

${\displaystyle \angle QCB=\angle QBA=\angle QAC=\omega .\,}$

எனவே இரு பிரகார்டு கோணங்களும் சமவளவானவை.

இரு பிரகார்டு புள்ளிகளும் நெருங்கிய தொடர்புள்ளவை. ABC முக்கோணத்தின் கோணங்கள் எடுத்துக்கொள்ளப்படும் வரிசைப்போக்கைப் பொறுத்து இப்புள்ளிகள் மாறுபடுகின்றன. எடுத்துக்காட்டாக முக்கோணம் ABC இன் முதல் பிரகார்டு புள்ளியானது முக்கோணம் ACB இன் இரண்டாவது பிரகார்டு புள்ளியாக இருக்கும்.

முக்கோணம் ABC இன் இரு பிரகார்டு புள்ளிகளும் ஒன்றுக்கொன்று சமகோண இணையியங்கள் ஆகும்.

இரு பிரகார்டு புள்ளிகளும் முக்கோண மையங்கள் அல்ல. அவை இரண்டும் வடிவொத்த உருமாற்றங்களைப் பொறுத்து மாறாநிலை கொண்டவையல்ல. எனினும் வரிசையற்ற சோடியாக எடுத்துக்கொள்ளப்படும் பிரகார்டு புள்ளிகள் வடிவொப்புமைகளின்கீழ் மாறாநிலை கொண்டிருக்கும். ஒரு அசமபக்க முக்கோணத்தின் ஒரு பிரகார்டு புள்ளியை மற்றொரு பிரகார்டு புள்ளியாக மாற்றும் எதிரொளிப்பு ஒரு சிறப்புவகை வடிவொப்புமை ஆகும்.

ஒரு முக்கோணத்தின் முதல் பிரகார்டு புள்ளியைக் காண்பதற்கான வரைமுறை கீழே தரப்பட்டுள்ளது.

• முக்கோணம் ABC இன் இரு உச்சிகள் A, B வழியாகச் செல்லுமாறும், முக்கோணத்தின் பக்கம் BC ஐத் தொடுகோடாகவும் கொண்டவாறும் ஒரு வட்டம் வரையப்படுகிறது. இவ்வட்டத்தின் மையப்புள்ளியானது AB இன் நடுக்குத்துக்கோடும், B வழியாக BC க்கு செங்குத்தாக வரையப்பட்ட கோடும் சந்திக்கும் புள்ளியாக இருக்கும்.

• இதேபோல B, C உச்சிகள் வழியாகவும், பக்கம் AC ஐத் தொடுமாறு ஒரு வட்டமும், A, C உச்சிகள் வழியாகவும் பக்கம் AB ஐத் தொடுமாறு மற்றுமொரு வட்டமும் வரையப்படுகிறது

• இம்மூன்று வட்டங்களும் ஒரு புள்ளியில் சந்திக்கின்றன. அப்பொதுப்புள்ளியே ABC முக்கோணத்தின் முதல் பிரகார்டு புள்ளியாகும்.

இதேமுறையில் இரண்டாவது பிரகார்டு புள்ளியைக் காணலாம்.

ஒரு முக்கோணத்தின் முதலாவது மற்றும் இரண்டாவது பிரகார்டு புள்ளிகளின் நடுப்புள்ளியானது பிரகார்டு நடுப்புள்ளி (Brocard midpoint) எனப்படும். முதலாவது மற்றும் இரண்டாவது பிரகார்டு புள்ளிகள் முக்கோண மையங்கள் அல்ல என்றாலும் பிரகார்டு நடுப்புள்ளி ஒரு முக்கோண மையமாக அமைகிறது.

முதல் பிரகார்டு புள்ளியின் முந்நேரியல் ஆயதொலைவுகள்:

c/b : a/c : b/a

இரண்டாவது பிரகார்டு புள்ளியின் முந்நேரியல் ஆயதொலைவுகள்:

b/c : c/a : a/b

பிரகார்டு நடுப்புள்ளியின் முந்நேரியல் ஆயதொலைவுகள்:

sin(A + ω) : sin(B + ω) : sin(C + ω)[1]

மூன்றாவது பிரகார்டு புள்ளியின் முந்நேரியல் ஆயதொலைவுகள்:

a⁻³ : b⁻³ : c⁻³

(அல்லது)

csc(A − ω) : csc(B − ω) : csc(C − ω),[2]

ஒரு முக்கோணத்தின் மூன்றாவது பிரகார்டு புள்ளியானது எதிர்நிரப்பு முக்கோணத்தின் பிரகார்டு நடுப்புள்ளியாக இருக்கும். மேலும் சமச்சரிவு இடைக்கோட்டுச் சந்தியின் சமவியல்பு இணையியமாகவும் இருக்கும்.

• Third Brocard Point at MathWorld
• Bicentric Pairs of Points and Related Triangle Centers
• Bicentric Pairs of Points
• Bicentric Points at MathWorld