பித்தாகரசின் சராசரிகள்

கணிதத்தில் முக்கியமான சராசரிகளான கூட்டுச் சராசரி (A), பெருக்கல் சராசரி (G), இசைச் சராசரி (H) ஆகிய மூன்றும் பித்தாகரசின் சராசரிகள் (Pythagorean means) என அழைக்கப்படுகின்றன. இம்மூன்றின் வரையறை:

$A(x_{1},\ldots ,x_{n})={\frac {1}{n}}(x_{1}+\cdots +x_{n})$
$G(x_{1},\ldots ,x_{n})={\sqrt[{n}]{x_{1}\cdots x_{n}}}$
$H(x_{1},\ldots ,x_{n})={\frac {n}{{\frac {1}{x_{1}}}+\cdots +{\frac {1}{x_{n}}}}}$

a மற்றும் b -ன் பித்தாகரசின் சராசரிகள் மற்றும் இருபடிச் சராசரியின் வடிவியல் வரைமுறை. H -இசைச் சராசரி, G -பெருக்கல் சராசரி, A -கூட்டுச்சராசரி, Q -இருபடிச் சராசரி.

இம்மூன்று சராசரிகளும் பின்வரும் பண்புகளைக் கொண்டுள்ளன:

மதிப்பு மாறாமை: $M(x,x,\ldots ,x)=x$
முதல் வரிசை சமச்சீர்தன்மை: $M(bx_{1},\ldots ,bx_{n})=bM(x_{1},\ldots ,x_{n})$
உள்மாற்றத்ததால் மாறாமை: $M(\ldots ,x_{i},\ldots ,x_{j},\ldots )=M(\ldots ,x_{j},\ldots ,x_{i},\ldots )$ .
$\min(x_{1},\ldots ,x_{n})\leq M(x_{1},\ldots ,x_{n})\leq \max(x_{1},\ldots ,x_{n})$

இம்மூன்று சராசரிகளும் வடிவவியலிலும் இசையிலும் அதிக முக்கியத்துவம் வாய்ந்தவையாக இருந்தமையால், முதலில் கணிதவியலாளர் பித்தாகரசாலும் பின் அவரைத் தொடர்ந்து கிரேக்க கணிதவியலாளர்களாலும் (தாமஸ் ஹீத், பண்டைய கிரேக்க கணித வரலாறு) ஆராயப்பட்டன.

இருபடிச் சராசரியுடன் தொடர்பு

இருபடிச் சராசரி: $Q={\sqrt {\frac {x_{1}^{2}+x_{2}^{2}+\cdots +x_{n}^{2}}{n}}}$ ) -ன் சேர்ந்து இவற்றின் வரிசைத் தொடர்பு:

\min \leq H\leq G\leq A\leq Q\leq \max

சராசரி காணப்படும் தரவின் உறுப்புகள் அனைத்தும் நேர்மமாக இருத்தல் வேண்டும். அனைத்து உறுப்புகளும் சமமாக இருந்தால் இருந்தால் மட்டுமே மேலே தரப்பட்ட வரிசைத் தொடர்பில் சமக்குறியீடு பொருந்தும். இச்சமனின்மையை கூட்டு மற்றும் பெருக்கல் சராசரிகளின் சமனின்மையின் பொதுமைப்படுத்தலாகவும் பொதுமைப்படுத்தப்பட்ட சராசரிகளின் சமனின்மையின் சிறப்பு வகையாகவும் கருதலாம்.

நிறுவல்: n = 2

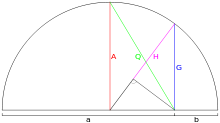
பக்கங்கள் (x, y, z), z -ஐக் கர்ணமாகக்கொண்ட செங்கோண முக்கோணங்களையும் பித்தாகரசின் தேற்ற முடிவையும் ( $x^{2}+y^{2}=z^{2}$ , $z>x$ , $z>y$ ) பயன்படுத்தி இச்சமனின்மையை n = 2 எனும்போது, அதாவது a, b என்ற இரு எண்களுக்கு நிறுவலாம்.[1]

செங்கோண முக்கோணங்கள்:

: $\left({\frac {b-a}{b+a}}{\sqrt {ab}},{\frac {2ab}{a+b}},{\sqrt {ab}}\right)=\left({\frac {b-a}{b+a}}{\sqrt {ab}},H(a,b),G(a,b)\right),$

இதிலிருந்து $H(a,b)<G(a,b)$ என அறியலாம.---------->1

: $\left({\frac {b-a}{2}},{\sqrt {ab}},{\frac {a+b}{2}}\right)=\left({\frac {b-a}{2}},G(a,b),A(a,b)\right),$

இதிலிருந்து $G(a,b)<A(a,b)$ என அறியலாம்.----------->2

: $\left({\frac {b-a}{2}},{\frac {a+b}{2}},{\sqrt {\frac {a^{2}+b^{2}}{2}}}\,\right)=\left({\frac {b-a}{2}},A(a,b),Q(a,b)\right),$

இதிலிருந்து $A(a,b)<Q(a,b)$ என அறியலாம்.------------->3

இம்மூன்றையும் பயன்படுத்த:

\min \leq H\leq G\leq A\leq Q\leq \max

மேற்கோள்கள்

Kung, Sidney H., "The Harmonic mean—geometric mean—arithmetic mean—root mean square inequality II," in Roger B. Nelsen, Proofs Without Words, The Mathematical Association of America, 1993, p. 54.

வெளி இணைப்புகள்

Pythagorean means on MathWorld

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Kung, Sidney H., "The Harmonic mean—geometric mean—arithmetic mean—root mean square inequality II," in Roger B. Nelsen, Proofs Without Words, The Mathematical Association of America, 1993, p. 54.