நிறை மையம்
இயற்பியலில், பரவெளியிலிருக்கும் ஒரு நிறை பரவலின் நிறை மையம் (அ) திணிவு மையம் என்பது பரவியுள்ள அந்த நிறைகளின் எடையிடப்பெற்ற ஒப்பு நிலைகளின் கூட்டல் சூனியமாகும் ஒரு தனித்தன்மையான புள்ளியாகும். அப்புள்ளியில் விசையளித்து உந்தப்படுமாயின், அந்தத் திணிவு சுழற்சியின்றி, விசையளிக்கப்பட்ட திசையில் நகரும். நிறை மையத்தைச் சுற்றியே ஒரு பொருளின் மொத்த நிறையும் சமச்சீராக பரவி இருக்கும்; அந்நிறை பரவலின் நிலை அளக்கூறுகளின் எடையிடப்பட்ட சராசரியே அப்பொருளின் நிலை அளக்கூறைக் குறிக்கும். விசையியலின் கணக்கீடுகள் பலவற்றை எளிமையாக்க, நிறை மையத்தின் அடிப்படையில் பெரும்பாலான சூத்திரங்கள் வகுக்கப்படுகின்றன.

ஓர் ஒற்றைத் திடப் பொருளைக் கருதினால், அதன் நிறை-மையம் பொருளின் உடல்வடிவில் நிலைத்ததாய் அமைந்திருக்கும்; அப்பொருள் சீரான அடர்த்தி கொண்டிருப்பின், நிறை-மையம், அப்பொருளின் வடிவியல் திணிவு மையத்தில் இடம் பெறும். குதிரை லாடம் போல ஓட்டையுடைய அல்லது திறந்த-வடிவ பொருட்களில், மேலும் சில குறிப்பிட்ட வகை பொருட்களில் நிறை-மையம் பொருளுடலுக்கு வெளியிலும் அமையப்பெறும். சூரியக் குடும்பத்துக் கோள்கள் போல, பல பொருட்கள் பரவியிருக்கும் பொழுது, அதிலிருக்கும் எந்தவொரு தனிப்பட்ட பொருளின் நிலையைப் பொருத்தும் நிறை-மையம் அமையாது.
விண்வெளியில் பரவியிருக்கும் கிரகக் கோள்கள் போன்ற நிறைகளின் உந்தம், வளைவுந்தம் போன்ற விசையியல் கணக்கீடுகளுக்கும் திடப் பொருள் இயக்கவியல் கணக்கீடுகளுக்கும், நிறை-மையம் ஒரு பயம்பெறும் குறிப்புப் புள்ளியாக விளங்குகிறது. சுற்றுப்பாதை விசையியலிலும், கோள்களின் அசைவு சமன்பாடுகள், நிறை-மையத்தில் இடம் பெறும் பல புள்ளி நிறைகளாக முறைபடுத்தப்படுகின்றன.நிறை-மையச் சட்டம் என்பது, ஓர் ஒருங்கிய அமைப்பமுறையின் நிறை-மையம், அதன் தோற்ற ஆள்கூற்று முறைமையைப் பொருத்தமட்டில், அசைவற்றிருக்கும் ஒரு நிலைமச் சட்டம்.
வரலாறு
"நிறை மையம்" என்பதன் கருத்துருவை ஈர்ப்புவிசை மைய வடிவமாக முதன்முதலில் பண்டைய கிரேக்க இயற்பியலாளர், கணிதரும் பொறியியலாளருமான, ஆர்க்கிமிடீஸ் அறிமுகப்படுத்தினார். அவர், ஈர்ப்பு விசை களத்தைச் சீரானதென கருதும்படியான எளிய அனுமானங்களின் அடிப்படையில் தம் ஆய்வுப் பணிகளை மேற்கொண்டார் - விளைவாக, தற்போது நிறை மையம் என்றழைக்கப்படுவதன் கணிதப் பண்புகளை வகுத்தார். ஒரு நெம்புகோலின் பல புள்ளிகளில் வைக்கப்பட்ட எடைகள் அதற்கு வழங்கிய முறுக்கு விசை, அந்நெம்புகோலின் நிறைமையம் என்ற ஒற்றைப் புள்ளியில் அவ்வெடைகளை வைத்தபோது வழங்கியதற்கு இணையாக இருக்கிறது என்பதை நிறுவினார். மிதக்கும் பொருட்கள் குறித்த ஆய்வுகளில் மிதவை பொருளின் நிறைமையத்தை இயன்றவரை கீழாக வைத்திருப்பதாகவே அதன் நோக்குநிலை அமைந்திருக்கும் என்று நிறுவினார். அவர், சீரான அடர்த்தியுடைய வரையறுக்கப்பட்ட வடிவிலான பல பொருட்களின் நிறைமையத்தைக் கணிக்கும் கணித நுட்பங்களை உருவாக்கினார்.[1]
நிறை மையம் பற்றிய கொள்கை பனைவுகளை ஆக்கிய பிந்திய கணிதவியலாளர்களுள் அலெக்சான்ட்ரியாவின் பாப்பஸ், குயீடோ உபால்டி, ஃபிரான்செஸ்கோ மௌரோலிகோ,[2] ஃபெடெரிகோ கமாண்டினோ,[3] சைமன் ஸ்டெவின்,[4] லுயூகா வேலெரியோ,[5] யான்-சார்லஸ் டெ லா ஃபெய்ல், பால் குல்டின்,[6] ஜான் வால்லிஸ், லூயி கார்ர், பியெர்ர் வாரிநன் மற்றும் அலெக்ஸிஸ் கிலெய்ரௌட் ஆகியோரும் அடங்குவர்.[7]
நியூட்டனின் இரண்டாம் விதி, ஆய்லரின் முதல் விதியின் நிறைமையத்தைக் கொண்டு மறு ஆக்கம் செய்யப்பட்டது.[8]
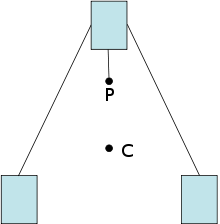
விளக்கம்
நிறை மையம் (அ) திணிவு மையம் என்பது பரவியுள்ள நிறைகளின் எடையிடப்பெற்ற ஒப்பு நிலை திசையன்களின் கூட்டல் சூனியமாகக்கூடிய, பரவெளி நிறை பரவலின் மத்தியில் இருக்கும் ஒரு தனித்தன்மையான புள்ளியாகும். புள்ளியியலோடு ஒப்புநோக்கினால், நிறைமையமானது ஒரு நிறை பரவலின் சராசரி இட அமைவாகக் கருதப்படும்.
துகள்களின் ஓர் ஒருங்கியம்
Pi, i = 1, …, n , என்ற துகள்களின் ஒருங்கியத்தில், ஒவ்வொன்றிற்கும் mi எடையுள்ள துகள்கள், வெளியில் ri, i = 1, …, n,என்ற ஆள்கூறுகளில் இடம்பெறுகையில் நிறைமையத்தின் ஆள்கூறுகளான R பின் வரும் சமன்பாட்டுள் பொருந்தும்
இச்சமன்பாட்டைத் தெளிகையில் R-ஆனது பின் வருமாறு கிடைக்கும்
இதில் M அனைத்துத் துகள்களின் கூட்டல் ஆகும்.
ஓர் இடையறாத தொகுதி
நிறை பரவலானது, இடையறாத ρ(r) என்ற அடர்த்தியுடைய, V என்ற கொள்ளளவுடய தொகுதிக்குள் இருக்குமாயின், அத்தொகுதிக்குள் நிலைமையமான R-இனைப் பொருத்து அமைந்திருக்கும் புள்ளிகளின் நிலைக் கூறுகளின் தொகையீடு சூனியம். அதாவது,
இச்சமன்பாட்டைத் தெளிகையில் R நிலைகூறுகளாகக் கிடைக்கப்பெறுவது,
இதில் M-ஆனது அத்தொகுதியில் இருக்கும் மொத்த நிறை.
ஓர் இடையறாத நிறை பரவல், சீரான, அதாவது ρ மாறா அடர்த்தியோடு அமைந்திருக்குமாயின், அத்தொகுதியின் வடிவியல் திணிவு மையமே அதன் நிறைமையமாக அமையும்.[9] நிறை பரவலை சமமான இரு பகுதிகளாகப் பிரிக்கும் தளம் அமையும் புள்ளி அன்று நிறைமையம். புள்ளியியலோடு ஒப்புநோக்கினால் இடைநிலையளவும் கூட்டுச்சராசரியும் ஒன்றல்லாதது போலாகும்.
கனமைய ஆள்கூறுகள்
P1 மற்றும் P2, எனும் m1 மற்றும் m2 நிறையளவுடைய, ஓர் இரு-துகள் ஒருங்கமைப்பின் நிறைமைய ஆள்கூறுகளான R-ஐப் பின்வரும் சமன்பாட்டால் பெறலாம்
மொத்த நிறையும், இவ்விரு துகள்களுக்கிடையில் பிரிந்திருக்கும் சதவிகிதம் 100% P1 மற்றும் 0% P2 -இல் இருந்து 50% P1 மற்றும் 50% P2 -இல் இருந்தும் 0% P1 மற்றும் 100% P2, வரையிலும் வேறுபடும் வேளையில், அவற்றின் நிறைமையமான R, P1 முதல் P2 வரையிலான நேர்கோட்டில் அமையும். அதன் ஒவ்வொரு புள்ளியிலும் காணப்பெறும் நிறை-விகிதங்கள், அக்கோட்டில் தெரியவரும் R புள்ளியின் வீச்ச ஆள்கூறுகள் (projective coordinates); இவற்றையே கனமைய ஆள்கூறுகள் என வழங்குவர். எதேச்சையான ஒரு புள்ளியினின்று இயங்கும் திருப்பங்களை இயக்கமுறையில் சமன் செய்வது, மற்றுமோர் விதத்தில் இச்செயல்முறையை விளக்குவதாகும். பின்ன மேலிலக்கம் பெறப்படும் மொத்த திருப்பத்தையும் குறிக்கும், நிறைமையத்தில் ஆற்றப்படும் ஓர் மொத்த நிகர்விசை அதனைச் சமன் செய்யும். தளத்திலும் பரவெளியிலும் வீச்ச ஆள்கூறுகளை விளக்க முறையே மூன்று மற்றும் நான்கு புள்ளிகளைக் கொண்டே இதனை அறியலாம்.
நிறைமையத்தைக் கண்டறிதல்
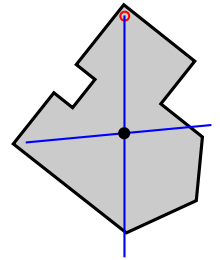
பயன்பாடுகள்
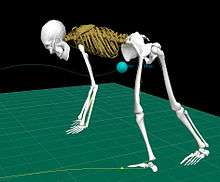
பொறியாளர்கள் பந்தய தானுந்துகளைச் சிறப்பாகக் கையாள வேண்டி அதன் நிறைமையம் தாழ்வாக அமையுமாறு வடிவமைப்பர். உயரம் தாண்டுவோர் "ஃபாஸ்பரி வீழ்ச்சி"யைச் செயலாற்றுகையில், தம் உடலின் நிறைமையம் தடுப்புக் கம்பியைத் தாண்டாதபோதும், தம் உடல் மட்டும் கம்பியைத் தாண்டுமாறு உடலை வளைப்பர்.[9]
வானூர்தி அறிவியல்
வானியல்
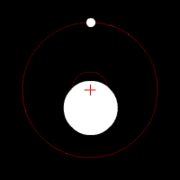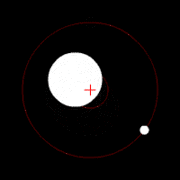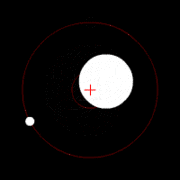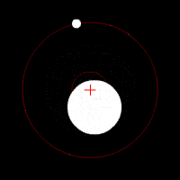
உடலியக்கவியல்
இவற்றையும் காண்க
- கனமையம்
- மேலுதைப்பு
- திணிவு மையம் (வடிவியல்)
- உருள் மையம்
குறிப்புகள்
- Shore 2008, பக். 9–11.
- Baron 2004, பக். 91–94.
- Baron 2004, பக். 94–96.
- Baron 2004, பக். 96–101.
- Baron 2004, பக். 101–106.
- Mancosu 1999, பக். 56–61.
- Walton 1855, பக். 2.
- Beatty 2006, பக். 29.
- Van Pelt 2005, பக். 185.
சான்றாதாரங்கள்
- Baron, Margaret E. (2004) [1969], The Origins of the Infinitesimal Calculus, Courier Dover Publications, ISBN 0-486-49544-2
- Beatty, Millard F. (2006), Principles of Engineering Mechanics, Volume 2: Dynamics—The Analysis of Motion, Mathematical Concepts and Methods in Science and Engineering, 33, Springer, ISBN 0-387-23704-6
- Feynman, Richard; Leighton, Robert; Sands, Matthew (1963), The Feynman Lectures on Physics, Addison Wesley, ISBN 0-201-02116-1
- Federal Aviation Administration (2007), Aircraft Weight and Balance Handbook (PDF), United States Government Printing Office, retrieved 23 October 2011
- Giambattista, Alan; Richardson, Betty McCarthy; Richardson, Robert Coleman (2007), College physics, 1 (2nd ed.), McGraw-Hill Higher Education, ISBN 0-07-110608-1
- Goldstein, Herbert; Poole, Charles; Safko, John (2001), Classical Mechanics (3rd ed.), Addison Wesley, ISBN 0-201-65702-3
- Hamill, Patrick (2009), Intermediate Dynamics, Jones & Bartlett Learning, ISBN 978-0-7637-5728-1
- Kleppner, Daniel; Kolenkow, Robert (1973), An Introduction to Mechanics (2nd ed.), McGraw-Hill, ISBN 0-07-035048-5
- Levi, Mark (2009), The Mathematical Mechanic: Using Physical Reasoning to Solve Problems, Princeton University Press, ISBN 978-0-691-14020-9
- Mancosu, Paolo (1999), Philosophy of mathematics and mathematical practice in the seventeenth century, Oxford University Press, ISBN 0-19-513244-0
- Murray, Carl; Dermott, Stanley (1999), Solar System Dynamics, Cambridge University Press, ISBN 0-521-57295-9
- Sangwin, Christopher J. (2006), "Locating the centre of mass by mechanical means" (PDF), Journal of the Oughtred Society, 15 (2), retrieved 23 October 2011
- Shore, Steven N. (2008), Forces in Physics: A Historical Perspective, Greenwood Press, ISBN 978-0-313-33303-3
- Symon, Keith R. (1971), Mechanics (3rd ed.), Addison-Wesley, ISBN 0-201-07392-7
- Van Pelt, Michael (2005), Space Tourism: Adventures in Earth Orbit and Beyond, Springer, ISBN 0-387-40213-6
- Walton, William (1855), A collection of problems in illustration of the principles of theoretical mechanics (2nd ed.), Deighton, Bell & Co.
- Asimov, Isaac (1988) [1966], Understanding Physics, Barnes & Noble Books, ISBN 0-88029-251-2
- Beatty, Millard F. (2006), Principles of Engineering Mechanics, Volume 2: Dynamics—The Analysis of Motion, Mathematical Concepts and Methods in Science and Engineering, 33, Springer, ISBN 0-387-23704-6
- Feynman, Richard; Leighton, Robert B.; Sands, Matthew (1963), The Feynman Lectures on Physics, 1 (Sixth printing, February 1977 ed.), Addison-Wesley, ISBN 0-201-02010-6
- Frautschi, Steven C.; Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (1986), The Mechanical Universe: Mechanics and heat, advanced edition, Cambridge University Press, ISBN 0-521-30432-6
- Goldstein, Herbert; Poole, Charles; Safko, John (2002), Classical Mechanics (3rd ed.), Addison-Wesley, ISBN 0-201-65702-3
- Goodman, Lawrence E.; Warner, William H. (2001) [1964], Statics, Dover, ISBN 0-486-42005-1
- Hamill, Patrick (2009), Intermediate Dynamics, Jones & Bartlett Learning, ISBN 978-0-7637-5728-1
- Jong, I. G.; Rogers, B. G. (1995), Engineering Mechanics: Statics, Saunders College Publishing, ISBN 0-03-026309-3
- Millikan, Robert Andrews (1902), Mechanics, molecular physics and heat: a twelve weeks' college course, Chicago: Scott, Foresman and Company, retrieved 25 May 2011
- O'Donnell, Peter J. (2015), Essential Dynamics and Relativity, CRC Press, ISBN 978-1-466-58839-4
- Pollard, David D.; Fletcher, Raymond C. (2005), Fundamentals of Structural Geology, Cambridge University Press, ISBN 0-521-83927-0
- Pytel, Andrew; Kiusalaas, Jaan (2010), Engineering Mechanics: Statics, 1 (3rd ed.), Cengage Learning, ISBN 978-0-495-29559-4
- Rosen, Joe; Gothard, Lisa Quinn (2009), Encyclopedia of Physical Science, Infobase Publishing, ISBN 978-0-8160-7011-4
- Serway, Raymond A.; Jewett, John W. (2006), Principles of physics: a calculus-based text, 1 (4th ed.), Thomson Learning, ISBN 0-534-49143-X
- Shirley, James H.; Fairbridge, Rhodes Whitmore (1997), Encyclopedia of planetary sciences, Springer, ISBN 0-412-06951-2
- De Silva, Clarence W. (2002), Vibration and shock handbook, CRC Press, ISBN 978-0-8493-1580-0
- Symon, Keith R. (1971), Mechanics, Addison-Wesley, ISBN 978-0-201-07392-8
- Tipler, Paul A.; Mosca, Gene (2004), Physics for Scientists and Engineers, 1A (5th ed.), W. H. Freeman and Company, ISBN 0-7167-0900-7
- Vint, Peter (2003), "LAB: Center of Mass (Center of Gravity) of the Human Body" (PDF), KIN 335 - Biomechanics, retrieved 18 October 2013
வெளியிணைப்புகள்
- Motion of the Center of Mass shows that the motion of the center of mass of an object in free fall is the same as the motion of a point object.
- The Solar System's barycenter, simulations showing the effect each planet contributes to the Solar System's barycenter.
- Center of Gravity at Work, video showing bjects climbing up an incline by themselves.