நறுக்கம்
யூக்ளியிய வடிவவியல், நறுக்கம் (shear அல்லது shear mapping) என்பது ஒரு நேரியல் கோப்பு ஆகும். இவ்வுருமாற்றத்தின் கீழ் யூக்ளிடிய தளத்தின் ஒவ்வொரு புள்ளியும் ஒரு குறிப்பிட்ட திசையில் நகர்த்தப்படும். நகர்த்தப்படும் அளவு, அத்திசைக்கு இணையான ஒரு நிலைக்கோட்டிற்கும் அப்புள்ளிக்குமான குறியிடப்பட்ட தூரத்தின் மடங்கின் விகிதவளவாக இருக்கும்.[1]

எடுத்துக்காட்டு:
ஆள்கூற்றுகள் கொண்ட ஒரு புள்ளியை புள்ளிக்கு மாற்றும் கோப்பு ஒரு நறுக்கமாகும். இதில் நகர்வு கிடைமட்டமாக உள்ளது. -அச்சு நிலைக்கோடு; புள்ளியின் ஆள்கூறு குறியிடப்பட்டத் தூரம். நிலைக்கோட்டிற்கு இருபுறமும் அமையும் புள்ளிகள், கோட்டின் மாற்றுப்புறத்திற்கு நகர்த்தப்படுகின்றன.
நறுக்கத்தைச் சுழற்சியாகத் தவறாகக் கருதிவிடக் கூடாது. ஒரு நறுக்கத்தின் கீழ் ஒரு தளத்தின் புள்ளிகளின் ஒரு தொகுதியில், அப்புள்ளிகளுக்கிடையேயுள்ள கோணங்கள் அனைத்தும் மாறுபடும்; நகர்வின் திசைக்கு இணையாக இல்லாத அப்புள்ளிகளின் கோட்டுத்துண்டுகளின் நீளங்களும் மாறுபடும். இதனால் நறுக்கத்தினால் வடிவவியல் வடிவங்கள் மாறுபடுகின்றன. எடுத்துக்காட்டாக, சதுரங்கள் இணைகரங்களாகவும் வட்டங்கள் நீள்வட்டங்களாகவும் உருமாறும். எனினும் நறுக்கத்தால் வடிவவியல் வடிவங்களின் பரப்பளவு மாறுவதில்லை; ஒருகோட்டுப்புள்ளிகளுக்கு இடைப்பட்ட சார் தூரங்களும் மாறுவதில்லை.
முப்பரிமாண வடிவவியலிலும் நறுக்கம் இதேமுறையில் வரையறுக்கப்படுகிறது. இடைப்பட்ட தூரம் நிலைக்கோட்டிற்குப் பதில் நிலையான தளத்திலிருந்து அளவிடப்படுகிறது. முப்பரிமாண நறுக்கத்தில் திட வடிவங்களின் கனவளவு பாதுகாக்கப்படுகிறது; ஆனால் நகர்விற்கு இணையான தளவடிவங்கள் தவிர்த்த பிற தளவடிவங்களின் பரப்பளவு மாற்றமடைகிறது.
பொதுவாக -பரிமாண கார்ட்டீசியன் வெளி இல் தூரமானது, நகர்வின் திசைக்கு இணையான, நிலையான மீத்தளத்திலிருந்து (hyperplane) அளக்கப்படுகிறது. இன் எந்தவொரு கணத்தின் -பரிமாண அளவைப் (மீக்கனவளவு) பாதுகாக்கும் ஒரு நேரியல் கோப்பாக இந்த வடிவவியல் உருமாற்றம் அமைகிறது.
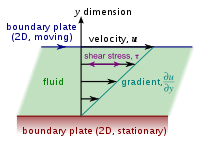
ஒன்றுக்கொன்று இணையாகவும், ஒன்றின் மேற்பக்கமாக மற்றது உள்ளதாகவுமான இரு தகடுகளுக்கு இடைப்பட்ட ஒரு பாய்மத்தின் வரிச்சீர் ஓட்டத்தை விளக்க நறுக்கம் பயன்படுகிறது.
வரையறை
ஒரு தளத்தின் கிடைமட்ட, குத்து நறுக்கம்
தளம் இல் கிடைமட்ட நறுக்கம் (horizontal shear) (அல்லது x அச்சுக்கு இணையான நறுக்கம்) என்பது ஆள்கூறுகள் கொண்ட பொதுவானதொரு புள்ளியை என்ற புள்ளிக்கு நகர்த்தும் சார்பாகும். இதில் நிலையான மதிப்புள்ள என்பது நறுக்கக் காரணியாகும் (shear factor).
இக்கோப்பால் ஒவ்வொரு புள்ளியும் அதன் ஆள்கூற்றின் விகிதவளவு கிடைமட்ட திசையில் நகர்த்தப்படுகிறது.
கிடைமட்ட நறுக்கத்தில்,
- -அச்சுக்கு மேற்புறம் அமையும் ஒவ்வொரு புள்ளியும் எனும்போது வலப்புறமும், எனும்போது இடப்புறமும் நகர்த்தப்படுகிறது; இதற்கு எதிர்மாறான திசையில் -அச்சுக்குக் கீழ்புறம் அமையும் புள்ளிகள் நகர்த்தப்படுகின்றன; -அச்சின் மீதமையும் புள்ளிகள் நிலையாக உள்ளன.
- -அச்சுக்கு இணையான கோடுகள் இடம் மாறாமல் நிலையாக இருக்கும். அதே சமயம் ஏனைய கோடுகள் அவை -அச்சை வெட்டும் புள்ளியைப் பொறுத்து பல்வேறு கோணங்களில் திருப்பமடைகின்றன. குறிப்பாகக் குத்துக்கோடுகள், சாய்வு கொண்ட சாய்ந்த கோடுகளாக மாற்றமடைகின்றன. குத்துக்கோடுகள் திருப்பப்படும் கோணம் நறுக்கக் கோணம் எனப்படும். நறுக்கக் கோணத்தின் கோடேன்ஜெண்ட் மதிப்பு நறுக்கக் காரணி க்குச் சமமாக இருக்கும்.
- ஒரு புள்ளியின் ஆள்கூறுகளை ஒரு நிரல் அணியாக எழுதினால் (2×1 அணி), நறுக்கத்தை 2x2 அணியின் பெருக்கலாக எழுதலாம்:
மற்றும் அச்சுகளின் பரிமாற்றம் தவிர, குத்து நறுக்கம் (vertical shear) (-அச்சுக்கு இணையான நறுக்கம்) கிடைமட்ட நறுக்கம் போன்றதாக இருக்கும்.
குத்து நறுக்கத்தில்:
- -அச்சுக்கு வலப்புறம் அமையும் ஒவ்வொரு புள்ளியும் எனும்போது மேற்புறமும், எனும்போது கீழ்ப்புறமும் நகர்த்தப்படுகிறது; இதற்கு எதிர்மாறான திசையில் -அச்சுக்கு இடப்புறம் அமையும் புள்ளிகள் நகர்த்தப்படுகின்றன; -அச்சின் மீதமையும் புள்ளிகள் நிலையாக உள்ளன.
- -அச்சுக்கு இணையான கோடுகள் (குத்துக்கோடுகள்) இடம் மாறாமல் நிலையாக இருக்கும். அதே சமயம் ஏனைய கோடுகள் அவை -axis அச்சை வெட்டும் புள்ளியைப் பொறுத்து பல்வேறு கோணங்களில் திருப்பமடைகின்றன. குறிப்பாகக் கிடைமட்டக் கோடுகள், சாய்வு கொண்ட சாய்ந்த கோடுகளாக மாற்றமடைகின்றன.
- ஒரு புள்ளியின் ஆள்கூறு அணியானது, கிடைமட்ட நறுக்கத்தில் பெருக்கப்படும் 2x2 அணியின் இடமாற்று அணியால் பெருக்கப்படுகிறது:
மேற்கோள்கள்
- Definition according to Weisstein, Eric W. Shear From MathWorld − A Wolfram Web Resource
