குவிச் சேர்வு

குவி வடிவவியலில், ஒரு குவிச் சேர்வு (convex combination) என்பது புள்ளிகளின் நேரியல் சேர்வுகளில் ஒரு சிறப்பு வகையாகும். இப்புள்ளிகள் திசையன்களாகவோ, திசையிலிகளாகவோ அல்லது இன்னும் பொதுவாக கேண்முறை வடிவவியல் புள்ளிகளாகவோ இருக்கலாம். குவிவுச் சேர்வாக அமையும் நேரியல் சேர்வில் கெழுக்களின் கூடுதல் 1 ஆக இருக்கும்.

ஒரு தளத்தில் தரப்பட்ட மூன்று புள்ளிகள் ${\displaystyle x_{1},x_{2},x_{3}.}$ இம்மூன்று புள்ளிகளின் குவிச் சேர்வு தரும் புள்ளி ${\displaystyle P}$ . ஆனால் ${\displaystyle Q}$ குவிச் சேர்வு அல்ல.
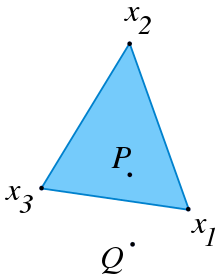
(எனினும் ${\displaystyle Q,}$ இம்மூன்று புள்ளிகளின் கேண்முறை சேர்வாக அமையும். ஏனென்றால் கேண்முறை மேற்தளம், எடுத்துக்கொணட முழுத் தளமாக அமையும்.)

மெய்யெண் திசையன் வெளியில் அமைந்த முடிவுறு எண்ணிக்கையிலான புள்ளிகள்:

${\displaystyle x_{1},x_{2},\dots ,x_{n}\,}$ .

இப்புள்ளிகளின் குவிச் சேர்வு பின்வருமாறுள்ள ஒரு புள்ளியாகும்:

${\displaystyle \alpha _{1}x_{1}+\alpha _{2}x_{2}+\cdots +\alpha _{n}x_{n}}$

இங்கு மெய்யெண்களான ${\displaystyle \alpha _{i}\,}$

${\displaystyle \alpha _{i}\geq 0}$ மற்றும் ${\displaystyle \alpha _{1}+\alpha _{2}+\cdots +\alpha _{n}=1.}$ என்றவாறு அமையும்.

எடுத்துக்காட்டாக, இரு புள்ளிகளின் ஒவ்வொரு குவிச் சேர்வும் அவ்விரு புள்ளிகளை இணைக்கும் கோட்டுத்துண்டின்மீது அமையும் ஒரு புள்ளியாக இருக்கும். தரப்பட்ட புள்ளிகளின் குவிச் சேர்வுகள் அனைத்தும் அப்புள்ளிகளின் குவிவு மேற்தளத்துக்குள்ளாகவே(convex hull) அமையும். ஒரு கணத்திலுள்ள புள்ளிகளின் குவிச் சேர்வுகளின் தொகுப்பு, அக்கணத்தின் குவி மேற்தளமாக அமையும்.

நேரியல் சேர்வு என்ற செயலின்கீழ் அடைவு பெறாத, ஆனால் குவிச் சேர்வுகளுக்கு அடைவு பெற்ற உட்கணங்கள் திசையன் வெளியில் உண்டு.