எண் கோடு
அடிப்படைக் கணிதத்தில் எண்கோடு (number line) அல்லது மெய்யெண் கோடு (real line) என்பது ஒரு கிடைமட்டமாக வரையப்படும் கோடாகும். இக்கோட்டின் மீதுள்ள ஒவ்வொரு புள்ளியும் ஒரு மெய்யெண்ணைக் குறிக்கும். எண்கோட்டிற்கும் மெய்யெண் கணத்திற்குமிடையே ஒன்றுக்கு-ஒன்று தொடர்புள்ளது.[1]
மேலே தரப்பட்டுள்ள எண்கோட்டின் வரைபடத்தில் -9 முதல் 9 வரையிலான முழுஎண்களுக்கான புள்ளிகள் மட்டுமே காணப்பட்டாலும் இக் கோடு முடிவில்லாமல் இருபுறமும் நீண்டு அனைத்து மெய்யெண்களையும் குறிக்கும். எண்கோடு இரு சமச்சீரான இரு அரைப்பகுதிகளாக எண் சுழியால் பிரிக்கப்படுகிறது. சுழிக்கு இடப்புறமுள்ள பகுதி எதிர் எண்களையும், வலப்புறமுள்ள பகுதி நேர் எண்களையும் குறிக்கின்றன.
மெய்யெண் கணத்தைப் போலவே மெய்யெண் கோடும் R அல்லது என்ற குறியீட்டால் குறிக்கப்படுகிறது. சிலசமயங்களில் மெய்யெண்கோடானது, ஒருபரிமாண யூக்ளிடிய வெளி என்பதைக் காட்டுவதற்காக R1 எனவும் குறிக்கப்படுகிறது.
ஒன்றுக்கொன்று சேர்ப்பிலா, வெற்றற்ற திறந்த மெய்யெண் கோட்டின் இடைவெளிகள் எண்ணுறுமை கொண்டவையாக இருக்கும்.
வரைதல்
எண்கோடு வழக்கமாக ஒரு கிடைமட்டக் கோடாக வரையப்படுகிறது. நேர் முழுஎண்கள் சுழிக்கு வலப்புறமும், எதிர் முழுஎண்கள் இடப்புறமும் சீரான சம இடைவெளிகளிலான புள்ளிகளால் குறிக்கப்படுகின்றன. எண்கோடு இருபுறமும் முடிவில்லாமல் நீள்கிறது என்பதை வலியுறுத்த, கோட்டின் இருமுனைகளிலும் அம்புக்குறிகள் வரையப்படுகின்றன.
எண்கோட்டிலுள்ள சுழிப்புள்ளி வழியாக எண்கோட்டிற்குச் செங்குத்தாக வரையப்படும் கோடு கற்பனை எண்களைக் குறிக்கிறது. இவ்வாறு வரையப்படும் கோடானது, எண்கோட்டுடன் சேர்ந்து சிக்கலெண்களைக் குறிக்கும் சிக்கலெண் தளமாகிறது.
வடிவவியல் வெளியாக

மெய்யெண்கள் கணம் R இல் உள்ள அனைத்து மெய்யெண்களையும், மெய்யெண் கோடு கொண்டிருக்கிறது. ஒரு வடிவவியல் வெளியாக மெய்யெண் கோட்டைக் கருதலாம். ஒருபரிமாண யூக்ளிடிய வெளி, திசையன் வெளி, மெட்ரிக் வெளி, இடவியல் வெளி, அளவை வெளி அல்லது நேரியல் தொடரகம் ஆகிய வெளிகளாக மெய்யெண் கோட்டைக் கொள்ளலாம்.
நேரியல் தொடரகமாக
<, வரிசைப்படுத்தலின்படி மெய்யெண் கோடு ஒரு நேரியல் தொடரகம் (linear continuum) ஆகும். இந்த வரிசைப்படுத்தலின்படி மெய்யெண்கோடு அடர்த்தியாக, நேரியல் வரிசைப்படுத்தப்பட்டு, மீச்சிறு மேல்வரம்பும் கொண்டுள்ளது. மேலும்,
மெய்யெண் கோட்டிற்கு மீச்சிறு அல்லது மீப்பெரு உறுப்புகள் கிடையாது; எண்ணுறு உறுப்புகள் கொண்ட விகிதமுறு எண்கள் கணம் மெய்யெண் கோட்டின் ஒரு உட்கணமாகும் என்னும் இரு பண்புகளையும் இணைத்த கூற்றான,
’மீச்சிறு அல்லது மீப்பெரு உறுப்புகள் கொண்டிராத; எண்ணுறு உறுப்புகள் கொண்ட உட்கணமுடைய எந்தவொரு நேரியல் தொடரகமும் மெய்யெண் கோட்டுடன் வரிசைச் சம அமைவியம் கொண்டதாகும்’
என்பது ஒரு தேற்றமாகும்.
மெட்ரிக் வெளியாக
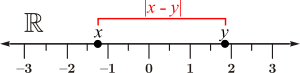
தனி வித்தியாசத்தைத் தரும் தொலைவுச் சார்பு d(x, y) = | x − y | உடன், மெய்யெண் கோடு ஒரு மெட்டிரிக் வெளியாகும். n-பரிமாண யூக்ளிடிய மெட்ரிக்கை n x n அலகு அணியால் குறிக்கலாம் என்பதால்,1 x 1 அலகு அணி, அதாவது 1 மெய்யெண் கோட்டின் மெட்ரிக்கைக் குறிக்கும்.
திசையன் வெளியாக
மெய்யெண் கணம் R என்ற களத்தின் மீதான ஒருபரிமாண திசையன் வெளியாக மெய்யெண் கோடு உள்ளது. மெய்யெண்களின் சாதாரணப் பெருக்கல் செயலை உட்பெருக்கமாகக் கொண்டு, இது ஒரு யூக்ளிடிய தளமாக உள்ளது. R இன் நெறிமம் தனி மதிப்புச் சார்பாகும்.
மேற்கோள்கள்
- James Stewart (mathematician); Redlin, Lothar; Watson, Saleem (2008). College Algebra (5th ). Brooks Cole. பக். 13–19. பன்னாட்டுத் தரப்புத்தக எண்:0-495-56521-0.
- James Munkres (1999). Topology (2nd ). Prentice Hall. பன்னாட்டுத் தரப்புத்தக எண்:0-13-181629-2.
- Walter Rudin, Real and Complex Analysis, McGraw-Hill, 1966, ISBN 0-07-100276-6.