இருவழிக்கோப்பு

${\displaystyle f:X\rightarrow Y}$ என்ற கோப்பு இருவழிக்கோப்பாவதற்கு இலக்கணம்:

${\displaystyle \forall y\in F,\,\exists x\in E,\,f(x)=y}$

இருவழிக்கோப்பு.

சுற்றுலாப்பயணிகளின் கூட்டமொன்று இராத்தங்க, எல்லா அறைகளும் காலியாக இருக்கும் ஒரு விடுதியில் வந்து சேருகின்றனர். ஒவ்வொரு பயணிக்கும் அறை வழ்ங்க வேண்டும், ஒரு பயணிக்கு ஒரேயொரு அறை வழங்க வேண்டும் ஆகிய விதிகளுக்கு உட்பட்டு அறைகள் வழங்கும் முறையை ஒருகோப்பாக விவரிக்கலாம். (பயணிகள் கணம்: X ; அறைகள் கணம்: Y.)

ஒவ்வொரு பயணிக்கும் ஒரு தனி அறை கிடைக்கவேண்டுமென்றால், அறைகளின் எண்ணிக்கை பயணிகளின் எண்ணிக்கையைவிடக் குறைவாக இருக்கக்கூடாது.அப்பொழுது ஒவ்வொரு பயணிக்கும் ஒரு தனி அறை கிடைக்கும். இது உள்ளிடுகோப்பு (injective map; injection; one-one map).

ஒவ்வொரு அறையும் நிரப்பப்படவேண்டுமென்றால், பயணிகளின் எண்ணிக்கை அறைகளின் எண்ணிக்கையைவிடக் குறைவாக இருக்கக்கூடாது. அப்பொழுது ஒவ்வொரு அறையிலும் குறைந்த பட்சம் ஒரு பயணியாவது இருப்பர். இது முழுக்கோப்பு (surjective map; surjection; onto map).

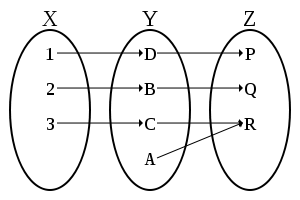
சில அறைகள் நிரப்பப்படாமலும், சில அறைகளில் ஒன்றுக்கு மேற்பட்ட பயணிகளும் இருக்கும்படி செய்யப்பட்ட கோப்பு, உள்ளிடுகோப்புமல்ல, முழுக்கோப்புமல்ல. இதை வெறும் உட்கோப்பு (into map) என்று மட்டும் சொல்லலாம்.

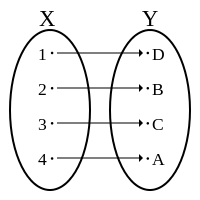
பயணிகளின் எண்ணிக்கையும் அறைகளின் எண்ணிக்கையும் சமமாக இருந்தால், ஒவ்வொரு பயணிக்கும் ஒரு தனி அறை கிடைக்கும். ஒரு அறையும் காலியாக இருக்காது. இது இருவழிக்கோப்பு (bijective map; bijection; one-one onto map). அதாவது, இது உள்ளிடுகோப்பு, முழுக்கோப்பு ஆகிய இரு பண்புகளையும் கொண்டது.

${\displaystyle f:\mathbf {R} \rightarrow \mathbf {R} }$

${\displaystyle f(x)=2x-1}$

இது ஒரு இருவழிக்கோப்பு. ஏனென்றால் y = 2x - 1 க்குச்சரியானதாக f இன் ஆட்களத்தில் ஒரே ஒரு ${\displaystyle (y+1)/2=x}$ இருக்கிறது.

மாறாக,

${\displaystyle g:\mathbf {R} \rightarrow \mathbf {R} }$

${\displaystyle g(x)=x^{2}}$

இருவழிக்கோப்பல்ல. இதற்கு இரண்டு காரணங்கள். ஒன்று அது உள்ளிடுகோப்பல்ல; ஏனென்றால், எடுத்துக்காட்டாக, ${\displaystyle g(1)=g(-1)}$

மற்றும் முழுக்கோப்புமல்ல; ஏனென்றால், எடுத்துக்காட்டாக, ${\displaystyle y=-1}$ க்கு முன்னுரு கிடையாது.

ஏதாவதொரு காரணமே அது இருவழிக்கோப்பல்ல என்பதற்குப் போதுமானது.

மாறாக, அதே சார்பு ${\displaystyle g}$ க்கு, ஆட்களத்தையும் இணையாட்களத்தையும் மாற்றி அமைத்து அதை இருவழிக்கோப்பாக்க முடியும்:

${\displaystyle h:\mathbf {R} ^{+}\rightarrow \mathbf {R} ^{+}}$

${\displaystyle h(x)=x^{2}}$

இது இருவழிக்கோப்பு. ஏனென்றால் ஒவ்வொரு ${\displaystyle y}$ க்கும் ஒரே ஒரு ${\displaystyle x=\surd y}$ என்ற முன்னுரு இருக்கிறது.

${\displaystyle f:Z\rightarrow Z}$ இங்கு Z முழுஎண்களின் கணம்.

${\displaystyle f(n)=n+1}$

இது ஒரு இருவழிக்கோப்பு.

${\displaystyle exp:\mathbf {R} \rightarrow \mathbf {R} }$

${\displaystyle f(x)=e^{x}}$

இருவழிக்கோப்பல்ல. ஏனென்றால், எடுத்துக்காட்டாக, ${\displaystyle \mathbf {R} }$ இல் ${\displaystyle f(x)=-1}$ க்குத் தீர்வு கிடையாது.

ஆனால், இணையாட்களத்தை ${\displaystyle \mathbf {R} ^{+}=(0,\infty )}$ க்கு மாற்றினால், அது இருவழிக்கோப்பாகும். அதனுடைய நேர்மாறு இயல்மடக்கைச்சார்பாகும்.

• ${\displaystyle f:\mathbf {R} \rightarrow [-1,1]}$

${\displaystyle f(x)=sinx}$

இது ஒரு இருவழிக்கோப்பல்ல; ஏனென்றால், எடுத்துக்காட்டாக, ஆட்களத்திலுள்ள ${\displaystyle \pi /6}$ , ${\displaystyle 5\pi /6}$ இரண்டும் 1/2 என்ற ஒரே மதிப்பிற்குச் செல்கிறது.

மாறாக,

• ${\displaystyle g:[-\pi /2,\pi /2]\rightarrow [-1,1]}$

${\displaystyle g(x)=sinx}$ இருவழிக்கோப்பாகிறது.

முதல் கோப்பு (g) உள்ளிடுகோப்பகவும், இரண்டாவது (f) முழுக்கோப்பாகவும் உள்ள சேர்வை ${\displaystyle f\circ g}$

• ${\displaystyle f:\mathbf {R} \rightarrow \mathbf {R} }$ ஒரு இருவழிக்கோப்பானால், அதனுடைய வரைவு ஒவ்வொரு கிடைக்கோட்டையும் ஒரே ஒரு புள்ளியில் சந்திக்கும்.

• ${\displaystyle f:X\rightarrow Y}$ ஒரு இருவழிக்கோப்பாக இருக்கவேண்டுமென்றால் அதற்கு இலக்கணமே:

${\displaystyle f\circ g:Y\rightarrow Y=I:Y\rightarrow Y}$

மற்றும் ${\displaystyle g\circ f:X\rightarrow X=I:X\rightarrow X}$ ஆக இருக்கும்படி

${\displaystyle g:Y\rightarrow X}$ என்ற ஒரு கோப்பு இருக்கவேண்டும்.

இந்த ${\displaystyle g}$ தான்${\displaystyle f}$ இன் நேர்மாற்றுக்கோப்பு. மற்றும் ${\displaystyle g}$ இன் நேர்மாறு ${\displaystyle f}$ .

• ${\displaystyle f\circ g}$ ஒரு இருவழிக்கோப்பனால், ${\displaystyle f}$ முழுக்கோப்பாகவும் ${\displaystyle g}$ உள்ளிடுகோப்பாகவும் இருந்தாகவேண்டும்.(படிமம் பார்க்கவும்)

• ${\displaystyle f}$ ம் ${\displaystyle g}$ ம் இருவழிக்கோப்பானால் ${\displaystyle f\circ g}$ இருவழிக்கோப்பே. மற்றும்

${\displaystyle (f\circ g)^{-1}=g\circ f}$

• ${\displaystyle X}$ இலிருந்து ${\displaystyle X}$ க்கே வரையறுக்கப்பட்ட எல்லா இருவழிக்கோப்புகளும் ' ${\displaystyle \circ }$ ' என்ற சேர்வை விதிக்கு ஒரு குலமாகும். இதை X இன் சமச்சீர்குலம் (Symmetric Group on ${\displaystyle X}$ ) என்பர். குறியீடு: S(X) அல்லது ${\displaystyle S_{X}}$

Xம் Yம் முடிவுறு கணங்களாக இருக்கும்போது Xஇலிருந்து Yக்கு ஒரு இருவழிக்கோப்பு இருக்குமானால், X இலுள்ள உறுப்புகளின் எண்ணிக்கையும் Y இலுள்ள உறுப்புகளின் எண்ணிக்கையும் சமமாக இருக்கவேண்டும்.

இவையே முடிவுறாகணங்களாக இருந்தால், இரண்டு கணங்களின் எண்ணளவைகள் ஒன்றாக இருக்கவேண்டும்.

• முழுக்கோப்பு
• உள்ளிடுகோப்பு