ஆர்க்கிமிடியச் சுருள்

ஆர்க்கிமிடியச் சுருள் அல்லது எண்கணிதச் சுருள் என்பது, ஒருவகைச் சுருள் ஆகும். இப்பெயர் கிமு மூன்றாம் நூற்றாண்டில் வாழ்ந்த ஆர்க்கிமிடிசு என்னும் கணிதவியலாளரின் பெயரைத் தழுவியது. மாறாக் கோணத் திசைவேகம் ஒன்றுடன் சுற்றும் ஒரு நேர்கோட்டில் மாறா வேகத்துடன் செல்லும் புள்ளியொன்றின் ஒழுக்கே ஆர்க்கிமிடியச் சுருள் ஆகும். முனைவாள்கூறுகளின் (r, θ) அடிப்படையில் இது பின்வரும் சமன்பாட்டால் குறிக்கப்படும்.

மூன்று 360° சுற்றுக்கள் கொண்ட ஒரு ஆர்க்கிமிடியச் சுருள்

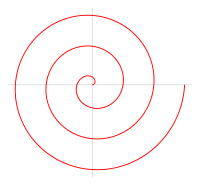
இங்கே a, b என்பன உண்மை எண்கள். a மாறும்போது சுருள் சுற்றும். அடுத்தடுத்த சுற்றுக்களுக்கு இடையிலான தூரம் b இல் தங்கியுள்ளது.

இயல்புகள்

ஆர்க்கிமிடியச் சுருள், மடக்கைச் சுருளில் இருந்து வேறுபட்டது. ஆர்க்கிமிடியச் சுருளில், அடுத்தடுத்த சுற்றுகளுக்கு இடையிலான தூரம் ஒரேயளவாக இருக்கும். θ வை ரேடியனில் அளந்தால், மேற்படி தூரம் 2πb ஆக இருக்கும். மடக்கைச் சுருளில் இந்தத் தூரம் பெருக்குத் தொடரில் அமைந்திருக்கும்.

பொதுவான ஆர்க்கிமிடியச் சுருள்

சில வேளைகளில் ஆர்க்கிமிடியச் சுருள் என்னும் சொல் பொதுவான சுருள்களின் தொகுதியைக் குறிக்கப் பயன்படுகிறது.

x = 1 ஆக இருக்கும்போது சாதாரண ஆர்க்கிமிடியச் சுருள் உருவாகிறது. மீவளையச் சுருள், பெர்மாவின் சுருள், ஊதுகொம்புத் தளவளைவு என்பன இத் தொகுதியுள் அடங்கும் பிற சுருள்கள் ஆகும். இயற்கையில் காணப்படும் நிலையான சுருள்கள் அமைத்தும் மடக்கைச் சுருள்களே. சூரியக் காற்றின் பார்க்கர் சுருள், கதரீன் சில்லினால் உருவாகும் கோலம் போன்ற இயங்கு சுருள்கள் ஆர்க்கிமிடியச் சுருள்கள் ஆகும்.

பயன்பாடு
சுருள்வடிவ அமுக்கியின் பொறிமுறை

ஆர்க்கிமிடியச் சுருள் பல தேவைகளுக்குப் பயன்படுகின்றது. சுருள்வடிவ அமுக்கிகளில் ஒன்றினுள் ஒன்று அமைந்த இரண்டு ஒரேயளவான ஆர்க்கிமிடியச் சுருள்கள் பயன்படுகின்றன. இது, வளிமங்களையும், நீர்மங்களையும் அமுக்குவதற்குப் பயன்படுகின்றது.[1] கைக்கடிகாரங்களில் பயன்படும் சமநிலைச் சுருள்கள் ஆர்க்கிமிடியச் சுருள்கள் ஆகும். பழங்காலத்து இசைத்தட்டுக்களில் காணப்படும் வரிப்பள்ளமும் ஆர்க்கிமிடியச் சுருள் வடிவினதே. இவ்வாறு, வரிப்பள்ளங்களை ஒரேயளவான இடைத்தூரத்தில் அமைப்பதன் மூலம் குறித்த பரப்பளவில் கூடிய இசைத் தகவல்களை அடக்க முடிந்தது. எனினும், ஒலித் தரத்தின் மேம்படுக்காக இது பிற்காலத்தில் மாற்றப்பட்டது.[2] நோயாளிகளை ஆர்க்கிமிடியச் சுருள் ஒன்றை வரையச் சொல்வது உடல் நடுக்கத்தை அளவிடுவதற்கான ஒரு முறையாகக் கையாளப்படுகிறது. இது நரம்பியல் நோய்களைக் கண்டறிவதில் உதவுகிறது.

குறிப்புகள்
  1. Sakata, Hirotsugu and Masayuki Okuda. "Fluid compressing device having coaxial spiral members". பார்த்த நாள் 2006-11-25.
  2. Penndorf, Ron. "Early Development of the LP". பார்த்த நாள் 2005-11-25.. See the passage on Variable Groove.

வெளியிணைப்புக்கள்
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.