அறுமுகத்திண்மம்
வடிவவியலில் ஆறுமுகங்கள் கொண்ட ஒரு பன்முகத்திண்மமானது, அறுமுகத்திண்மம் அல்லது அறுமுகி(hexahedron) என அழைக்கப்படுகிறது. ஆறுமுகங்களுமே சர்வசம சதுரங்களாக உள்ள ஓர் ஒழுங்கு அறுமுகத்திண்மம், கனசதுரமாகும்.
எடுத்துக்காட்டுகள்
அறுமுகத்திண்மங்களில் பல வகைகள் உண்டு. அவற்றில் சில, பரப்புருவில் கனசதுரத்திற்கு ஒத்ததாகவும், மற்றும் சில அவ்வாறு இல்லாமலும் அமைகின்றன. கீழுள்ள அட்டவணை, அறுமுகத்திண்மங்களின் சில எடுத்துக்காட்டுகளைத் தருகின்றது.
| இணைகர முகங்களுடையவை | ||||
|---|---|---|---|---|
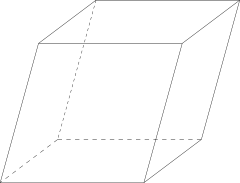 இணைகரத்திண்மம் (மூன்று சோடி இணைகரங்கள்) |
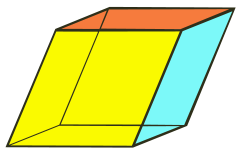 சாய்சதுரத்திண்மம் (மூன்று சோடி சாய்சதுரங்கள்) |
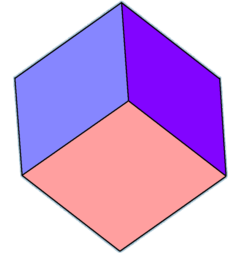 மூன்றுகோண பட்டமுகத்திண்மம் (சர்வசமமான சாய்சதுரங்கள்) |
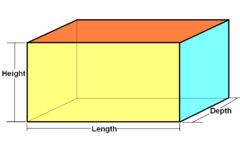 கனசெவ்வகம் (மூன்று சோடி செவ்வகங்கள்) |
 கனசதுரம் (சதுரம்) |
| மற்றவை | ||||
 ஐங்கோண பிரமிடு (ஐங்கோணம் மற்றும் முக்கோணங்கள்) |
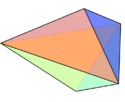 முக்கோண இரட்டைப்பிரமிடு (முக்கோணங்கள்) |
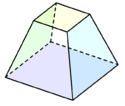 நாற்கர அடித்துண்டு (உச்சி-வெட்டப்பட்ட சதுரப்பிரமிடு) | ||
பரப்புருவில் மாறுபட்ட அறுமுகத்திண்மங்கள்
பரப்புருவில் மாறுபட்ட குவிவு அறுமுகத்திண்மங்கள் ஏழு உள்ளன.[1] அவற்றில் ஒன்று, இரண்டு கண்ணாடி பிரதிபிம்பங்களின் வடிவாக அமையும். (பன்முகத்திண்மங்களின் விளிம்புகளின் நீளங்கள், விளிம்புகள் மற்றும் முகங்களுக்கு இடையேயுள்ள கோணங்கள் இவற்றின் அளவை மாற்றுவதால் ஒன்றை மற்றொன்றாக மாற்றமுடியாதபடி, முகங்கள் மற்றும் உச்சிகளின் வித்தியாசமான் வரிசை அமைப்புகளைக் கொண்டிருக்கும் பன்முகத்திண்மங்கள், பரப்புருவில் மாறுப்பட்ட பன்முகத்திண்மங்கள் எனப்படும்.)
ஒவ்வொரு வகையின் எடுத்துக்காட்டுகள், கீழே அவற்றின் முகங்களின் பக்கங்கள், விளிம்புகள் மற்றும் உச்சிகளின் எண்ணிக்கையோடு தரப்பட்டுள்ளன:
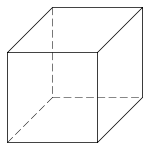 கனசதுரம், கனசெவ்வகம், இணைகரத்திண்மம் மற்றும் பிற.
|
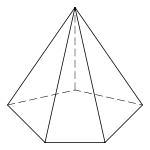 ஐங்கோண பிரமிடு
|

|
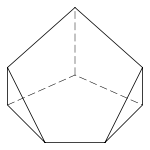
|
 முக்கோண இரட்டைப்பிரமிடு
|
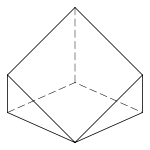
|
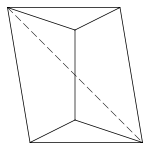 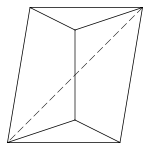 Tetragonal antiwedge. கைரல்(Chiral) – இடதுபுற மற்றும் வலதுபுற கண்ணாடி பிம்பங்களாக அமைகிறது.
| |
மேலும் மூன்று பரப்புருவில் வெவ்வேறான, குழிவு அறுமுகத்திண்மங்கள்:
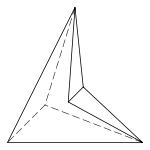
|

|
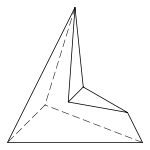
|
மேற்கோள்கள்
வெளி இணைப்புகள்
- Polyhedra with 4-7 Faces by Steven Dutch
- CM2 HexaMesh Hex-dominant Delaunay mesh generator.