कोणीय संवेग

भौतिक विज्ञान में कोणीय संवेग (Angular momentum), संवेग आघूर्ण (moment of momentum) या घूर्णी संवेग (rotational momentum)=[1][2] किसी वस्तु के द्रव्यमान, आकृति और वेग को ध्यान में रखते हुए इसके घूर्णन का मान का मापन है।[3] यह एक सदिश राशि है जो किसी विशेष अक्ष के सापेक्ष जड़त्वाघूर्ण व कोणीय वेग के गुणा के बराबर होता है। किसी कणों के निकाय (उदाहरणार्थ: दृढ़ पिण्ड) का कोणीय संवेग उस निकाय में उपस्थित सभी कणों के कोणीय संवेग के योग के तुल्य होता है।

चिरसम्मत यांत्रिकी

न्यूटन का गति का द्वितीय नियम
इतिहास · समयरेखा

चिरसम्मत यांत्रिकी में कोणीय संवेग

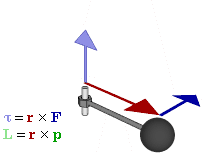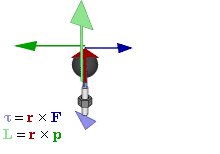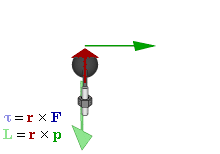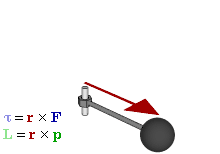
परिभाषा

किसी बिन्दु के सापेक्ष किसी 'कण' का कोणीय संवेग को सदिश गुणनफल के रूप में इस प्रकार अभिव्यक्त किया जा सकता है-

जहाँ उस बिन्दु के सापेक्ष उस कण का स्थिति सदिश है।

किसी अक्ष के सापेक्ष किसी कण का कोणीय संवेग उस अक्ष से कण तक के लम्बवत सदिश और उस कण के रैखिक संवेग के सदिश गुणनफल के बराबर होता है। ध्यान रहे कि कोणीय संवेग का मान, अक्ष के चुनाव पर निर्भर करता है (अलग-अलग अक्षों के सापेक्ष कोणीय संवेग भी अलग-अलग होगा), जबकि रेखीय संवेग का मान का अक्ष के चुनाव से कोई सम्बन्ध नहीं है।

किसी पिण्ड का कोणीय संवेग

किसी बिन्दु के सापेक्ष किसी पिण्ड का कोणीय संवेग उस बिन्दु के सापेक्ष उस पिण्ड के सभी कणों के कोणीय संवेग के सदिश योग के बराबर होता है।

किसी बिन्दु के सापेक्ष किसी पिण्ड का कोणीय संवेग = उस बिन्दु के सापेक्ष उस पिण्ड के द्रव्यमान केन्द्र का कोणीय संवेग + द्रव्यमान केन्द्र से जाने वाली अक्ष के सापेक्ष जड़त्वाघूर्ण x इस अक्ष के सापेक्ष कोणीय वेग

किसी अक्ष के सापेक्ष किसी गतिशील पिण्ड का कोणीय संवेग, उस अक्ष के सापेक्ष उस पिण्ड के जड़त्वाघूर्ण एवं उसके कोणीय वेग के गुणनफल के बराबर होता है।

कोणीय संवेग संरक्षण का नियम
नर्तकी का कोणीय संवेग अपरिवर्ती होने के कारण जब वह अपने हाथ-पैरों को बाहर फैला लेती है तो उसका कोणीय वेग कम हो जाता है। जब वह अपने हाथ-पैरों को सिकोड़ लेती है तो उसका जड़त्वाघूर्ण कम होता है और कोणीय संवेग संरक्षण के कारण उसका कोणीय वेग बढ़ जाता है।
यदि किसी निकाय पर कोई बाहरी बलाघूर्ण न लगाया जाय तो उस निकाय का कोणीय संवेग अपरिवर्तित रहता है।[4]

सन्दर्भ
  1. ट्रुसडेल, क्लिफोर्ड (1991). A First Course in Rational Continuum Mechanics: General concepts [परिमेय सातत्य यांत्रिकी में एक प्रथम पाठ्यक्रम: सामान्य अवधारणा] (अंग्रेज़ी में). एकेडेमिक प्रेस. पृ॰ 37. आई॰ऍस॰बी॰ऍन॰ 0-12-701300-8.
  2. स्मिथ, डोनाल्ड रे; ट्रुसडेल, क्लिफोर्ड (1993). An introduction to continuum mechanics – after Truesdell and Noll [सांतत्य यांत्रिकी का एक परिचय – ट्रुसडेल और नोल के बाद]. स्प्रिंगर. आई॰ऍस॰बी॰ऍन॰ 0-7923-2454-4.
  3. पिवार्स्की, जिम (2013). "Spin" [प्रचक्रण]. सिमिट्री मैगज़ीन.
  4. Conservation of Angular Momentum - Boundless

इन्हें भी देखें
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.