লগারিদম

গণিতের ক্ষেত্রে লগারিদম হলো সূচকের বিপরীত প্রক্রিয়া। এর অর্থ কোনো সংখ্যার লগারিদম হলো সেই সূচক যেটাকে একটি নির্ধারিত মানের, (ভিত্তি) ঘাত হিসাবে উন্নীত করলে প্রথমোক্ত সংখ্যাটি পাওয়া যায়। সাধারণ ক্ষেত্রে লগারিদম একটি সংখ্যা (ভিত্তি) কতবার গুণ করা হলো সেটা গণনা করে। উদাহরণস্বরূপ, ১০০০ এর ১০ ভিত্তিক লগের মান ৩, এর অর্থ হলো ১০ এর ঘাত ৩ এ উন্নীত করলে ১০০০ পাওয়া যায় ( $১০০০ = ১০ \times ১০ \times ১০ = ১০ ৩$ )। এখানে ১০ সংখ্যাটি ৩ বার গুণ করলে ১০০০ পাওয়া যায়। আরও সাধারণভাবে বলা যায়, কোনো ধনাত্মক প্রকৃত সংখ্যাকে যেকোনো প্রকৃত ঘাতে উন্নীত করলে সবসময় ধনাত্মক ফল পাওয়া যায়, সুতরাং যে কোনো দুটি ধনাত্মক প্রকৃত সংখ্যা $b$ এবং $x$ এর লগারিদম নির্ণয় করা যায় যেখানে $b$ সংখ্যাটি $১$ এর সমান নয়। $x$ এর $b$ ভিত্তিক লগকে প্রকাশ কর হয় এভাবে $log b (x)$ , এবং এর মান একটি অনন্য প্রকৃত সংখ্যা $y$ এমন যে,

b y = x

.

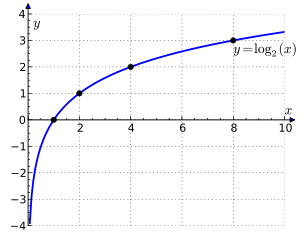
২ভিত্তিক লগারিদমের লেখচিত্র x অক্ষের (আনুভূমিক অক্ষ) ১ বিন্দুতে ছেদ করে এবং (২, ১), (৪, ২), এবং (৮, ৩) বিন্দু দিয়ে অতিক্রম করে।. উদাহরণস্বরূপ, log₂(8) = 3, কারণ 2³ = 8. রেখাটি ক্রমশ y অক্ষের নিকটবর্তী হতে থাকে কিন্তু কখনও yঅক্ষের সাথে মিলিত হয় না বা ছেদ করে না।.

একটি পূর্ণাঙ্গ 3-ary ট্রি ব্যবহার করে 3 এর সূচকগুলো প্রত্যক্ষ করা যায় এবং লগারিদমের সাথে সেগুলো কিভাবে সম্পর্কিত তা বোঝা যায়।

উদাহরণস্বরূপ, যেহেতু $৬৪ = ২ ৬$ , তাহলে আমরা পাই

log ২ (৬৪) = ৬

$১০$ ভিত্তিক লগারিদমকে (অর্থাৎ $b = ১০$ ) বলা হয় সাধারণ লগারিদম, বিজ্ঞান ও প্রকৌশল বিদ্যায় এর বহুবিধ ব্যবহার রয়েছে। প্রাকৃতিক লগারিদম এর ভিত্তি হলো একটি গাণিতিক ধ্রুবক E ( $\approx ২.৭১৮$ ); সহজ ডেরিভেটিভ (derivative) এর কারণে গণিত ও পদার্থবিদ্যায় এর বিস্তৃত ব্যবহার রয়েছে। দ্বিমিক লগারিদম এ ভিত্তি হিসাবে ব্যবহৃত হয় $২$ (অর্থাৎ $b = ২$ ) এবং এটা সাধারণভাবে কম্পিউটার বিজ্ঞান ব্যবহৃত হয়।

গণনা সহজ করার জন্য সপ্তদশ শতাব্দীর শুরুর দিকে জন নেপিয়ার লগারিদম এর সূচনা করেন। স্লাইড রুল এবং লগ সারণি ব্যবহার করে সহজে গণনার জন্য নাবিক, বৈজ্ঞানিক, প্রকৌশলী এবং অন্যান্যরা খুব দ্রুতই এগুলো গ্রহণ করেন। বিরক্তিকর বহুসাংখ্যিক গুণনের ধাপসমূহ লগারিদমের নিয়মে একটি সরল যোগে পরিণত হয়। লগারিদমের নিয়মানুযায়ী সংখ্যাসমূহের গুণফলের লগারিদম এর মান সংখ্যাগুলোর একক লগারিদমের মানের যোগফল। অর্থাৎ

\log _{b}(xy)=\log _{b}(x)+\log _{b}(y),\,

এখানে $b$ , $x$ and $y$ সকলে ধনাত্মক এবং $b \neq 1$ . বর্তমানের লগারিদমের ধারণা এসেছে লেওনার্ড অয়লার নিকট থেকে, যিনি অষ্টাদশ শতাব্দীতে লগারিদমকে সূচক অপেক্ষকের সূচক ফাংশন সাথে সম্পর্কযুক্ত করেন। যেকোন জটিল সংখ্যাকে A.e^iø, A≥0, আকারে প্রকাশ করা যায়। এই ধারণা থেকেই ঋণাত্মক সংখ্যা ও জটিল সংখ্যার লগারিদম সংজ্ঞায়িত করা যায়। তাহলে z একটি জটিল সংখ্যা হলে যদি এর মডুলাস |z|, আর্গুমেন্ট ø হয় তবে ln(z)=ln|z| +iø, এখন একটি জটিল সংখ্যার অসংখ্য আর্গুমেন্ট থাকে। কাজেই বলা যায় কোন সংখ্যার লগারিদমের অসংখ্য মান থাকতে পারে। তবে তার মুখ্য মান কেবল একটি। যেমন, z যদি ধনাত্মক সংখ্যা হয়, তবে |z|=z, মুখ্য আর্গুমেন্ট ø=0, কাজেই এর স্বাভাবিক লগারিদমের মুখ্য মান ln(z).

লগারিদম অভেদক

	সূত্র	উদাহরণ
গুণ	$\log _{b}(xy)=\log _{b}(x)+\log _{b}(y)$	$\log _{3}(243)=\log _{3}(9\cdot 27)=\log _{3}(9)+\log _{3}(27)=2+3=5$
ভাগ	$\log _{b}\!\left({\frac {x}{y}}\right)=\log _{b}(x)-\log _{b}(y)$	$\log _{2}(16)=\log _{2}\!\left({\frac {64}{4}}\right)=\log _{2}(64)-\log _{2}(4)=6-2=4$
ঘাত	$\log _{b}(x^{p})=p\log _{b}(x)$	$\log _{2}(64)=\log _{2}(2^{6})=6\log _{2}(2)=6$
মূল	$\log _{b}{\sqrt[{p}]{x}}={\frac {\log _{b}(x)}{p}}$	$\log _{10}{\sqrt {1000}}={\frac {1}{2}}\log _{10}1000={\frac {3}{2}}=1.5$

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.