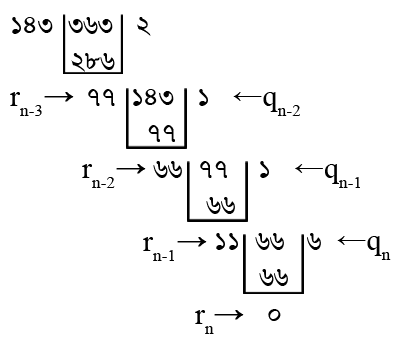গরিষ্ঠ সাধারণ গুণনীয়ক

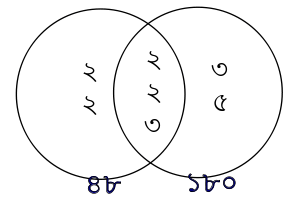
গ.সা.গু. মানে যেহেতু সবচেয়ে বড় সাধারণ উৎপাদক, তাই যেসব সংখ্যার গ.সা.গু. বের করতে হবে তাদের মৌলিক উৎপাদক (Prime factor) গুলো জানা থাকলে, সে সব মৌলিক উৎপাদক গুলোর মধ্যে যেগুলো সব গুলো সংখ্যার জন্য সাধারণ (common) সেগুলোকে নিয়ে গুন করলে ওই সংখ্যা গুলোর সবচেয়ে বড় সাধারণ উৎপাদক বা গ.সা.গু. পাওয়া যায়। উদাহরণ: ৪৮ এবং ১৮০ এর মৌলিক উৎপাদক গুলো হলো,

 ৪৮ = ২ × ২ × ২ × ২ × ৩
 ১৮০ = ২ × ২ × ৩ × ৩ ×৫

এখানে ৪৮ এবং ১৮০ এর জন্য দুটি ২ এবং একটি ৩ সাধারণ মৌলিক উৎপাদক, তাহলে ৪৮ এবং ১৮০ এর গ.সা.গু হলো ২×২×৩ = ১২।
নিচে ভেনচিত্রের মাধ্যমে উদাহরণটিকে আরো সুস্পষ্ট করে দেখানো হলো:

যদি সংখ্যাগুলোর কোন মৌলিক সাধারণ উৎপাদক না থাকে তবে তাদের গ.সা.গু. ১।

গ.সা.গু. নির্ণয়ের জন্য মৌলিক উৎপাদক পদ্ধতির চেয়ে অনেক বেশি কার্যকর পদ্ধতি হলো গ্রিক গণিতবিদ ইউক্লিডের[1] লিপিবদ্ধ করা ভাগ প্রক্রিয়ার এ পদ্ধতিটি। এটিকে ইউক্লিডের অ্যালগরিদম বলা হয়। এই অ্যালগরিদম বা প্রক্রিয়াটি এই পর্যবেক্ষণ থেকে এসেছে যে, দুটি সংখ্যা (a, b) (যেখানে a>b) এর গ.সা.গু. আর ((a-b), b) এর গ.সা.গু. একি হয়। যদি সংখ্যা গুলো যথাক্রমে ১৪৩ এবং ৭৭ হয় তাহলে, গসাগু(১৪৩, ৭৭) = গসাগু(৭৭, (১৪৩-৭৭)) = ১১। অর্থাৎ দুটি সংখ্যার গ.সা.গু. সংখ্যা দুটির পরমদূরত্বকেও নিঃশেষে ভাগ করে এবং সংখ্যা দুটির পরমদূরত্ব ও তাদের ক্ষুদ্রতম সংখ্যার গ.সা.গু. মূল সংখ্যা দুটির গ.সা.গু. এর সমান।
যদি এ পর্যবেক্ষণ সঠিক হয় তাহলে এই প্রক্রিয়াটি কিছু সংখ্যক বার পুনরাবৃত্তি করা হলে, মানে বড় সংখ্যাটি থেকে ছোট সংখ্যাটি বিয়োগ করে বিয়োগফল এবং ছোট সংখ্যাটি নিয়ে আবার একি কাজ করা হলে এক সময় বিয়োগফল এবং ছোট সংখ্যাটি সমান হয়ে যাবে, আর আমরা বুঝতে পারি দুটি সংখ্যা সমান হলে তাদের গরিষ্ঠ সাধারণ গুণনীয়ক হবে ওই সংখ্যাটিই। তাহলে অবশেষে আমরা মূল সংখ্যা দুটি এবং এই প্রক্রিয়ায় মধ্যবর্তী যতগুলো সংখ্যার জোড়া এসেছে তাদের সবার গ.সা.গু. পেয়ে যাবো। যেহেতু বারবার বিয়োগ করা মানে ভাগ করা তাই বিয়োগ না করে ছোট সংখ্যাটি দিয়ে বড় সংখ্যাটিকে ভাগ করে ভাগশেষ এবং ছোট সংখ্যাটি নিয়ে পুরো প্রক্রিয়াটিকে আরো দ্রুত শেষ করা সম্ভব। নিচে ভাগের মাধ্যমে ৩৬৩ এবং ১৪৩ এর গ.সা.গু নির্ণয়ের ধাপ গুলো দেখানো হলো:

উপরের ছবিতে ভাগশেষ গুলোকে ইংরেজি r এবং ভাগফল গুলোকে q দ্বারা চিহ্নিত করা হয়েছে।
বিধিসন্মত ভাবে ইউক্লিডের অ্যালগরিদমকে নিচের মতো করে বর্ণনা করা যায়:

${\displaystyle \operatorname {gcd} (a,0)=a}$

${\displaystyle \operatorname {gcd} (a,b)=\operatorname {gcd} (b,a-b\left\lfloor {a \over b}\right\rfloor ).}$

এটাকে আবার এই ভাবেও লেখা যায়:

${\displaystyle \operatorname {gcd} (a,0)=a}$

${\displaystyle \operatorname {gcd} (a,b)=\operatorname {gcd} (b,a{\mbox{ mod }}b).}$

ইউক্লিডের অ্যালগরিদমকে দুটি পর্যায়ক্রমিক যুক্তির মাধ্যমে প্রমাণ করা সম্ভব।

• প্রথম পর্যায়ে দেখানো হয় যে সর্বশেষ অ-শূন্য ভাগশেষ ${\displaystyle {r}_{n\mathrm {-} 1}}$ a এবং b দুটি সংখ্যাকেই নিঃশেষে ভাগ করে। যেহেতু a এবং b এর গ.সা.গু.(${\displaystyle g}$) ও ঠিক একি কাজ করে তাহলে ${\displaystyle {r}_{n\mathrm {-} 1}}$ কে অবশ্যই g এর চেয়ে ছোট বা সমান হতে হবে।
• দ্বিতীয় পর্যায়ে দেখানো হয় a এবং b এর যে কোন সাধারণ গুণনীয়ক (যার মধ্যে ${\displaystyle g}$ ও আছে) ${\displaystyle {r}_{n\mathrm {-} 1}}$ কে নিঃশেষে ভাগ করে, আর তাই যদি হয় তাহলে ${\displaystyle g}$ কে অবশ্যই ${\displaystyle {r}_{n\mathrm {-} 1}}$ এর চেয়ে ছোট অথবা সমান হতে হবে! আর এই দুটা প্রমাণ পরস্পরকে বাতিল করে দেয় যদি সর্বশেষ অ-শূন্য ভাগশেষ ${\displaystyle {r}_{n\mathrm {-} 1}}$ই গ.সা.গু. না হয় ।

${\displaystyle {r}_{n\mathrm {-} 1}}$ যে a এবং b এর গুণনীয়ক তা দেখানোর জন্য প্রথমে দেখানো হয় ${\displaystyle {r}_{n\mathrm {-} 1}}$ তার আগের ভাগশেষ ${\displaystyle {r}_{n\mathrm {-} 2}}$ এর গুণনীয়ক।

যেহেতু ${\displaystyle {r}_{n}\mathrm {=} 0}$

সেহতু ${\displaystyle {r}_{n\mathrm {-} 1}}$ অবশ্যই ${\displaystyle {r}_{n\mathrm {-} 2}}$ এর গুণনীয়ক, অর্থাৎ ${\displaystyle {r}_{n\mathrm {-} 2}\mathrm {=} {r}_{n\mathrm {-} 1}{q}_{n}}$

একি ভাবে বলা যায় ${\displaystyle {r}_{n\mathrm {-} 1}}$ অবশ্যই ${\displaystyle {r}_{n\mathrm {-} 3}}$ এরও গুণনীয়ক কারণ, ${\displaystyle {r}_{n\mathrm {-} 3}\mathrm {=} {r}_{n\mathrm {-} 2}{q}_{n\mathrm {-} 1}+{r}_{n\mathrm {-} 1}\mathrm {=} {r}_{n\mathrm {-} 1}{q}_{n}{q}_{n\mathrm {-} 1}+{r}_{n\mathrm {-} 1}\mathrm {=} \left({q}_{n}{q}_{n\mathrm {-} 1}+1\right){r}_{n\mathrm {-} 1}}$ এভাবে দেখানো যায় ${\displaystyle {r}_{n\mathrm {-} 1}}$ সব গুলো ${\displaystyle {r}_{x}}$ (x যেকোন ধনাত্মক সংখ্যা) এরই গুণনীয়ক। যেহেতু a এবং b কে ${\displaystyle {r}_{x}}$ হিসেবে বলা করা যায় সেহেতু প্রমাণিত হলো ${\displaystyle {r}_{n\mathrm {-} 1}}$ a এবং b দুটি সংখ্যাকেই নিঃশেষে ভাগ করে, অর্থাৎ ${\displaystyle {r}_{n\mathrm {-} 1}}$ a এবং b এর একটি সাধারণ গুণনীয়ক, আর তাই ${\displaystyle {r}_{n\mathrm {-} 1}\mathrm {\leq } g}$ হতে হবে

ধরা যাক a এবং b এর এটি সাধারণ গুননীয়ক হলো c সেক্ষেত্রে ${\displaystyle a\mathrm {=} {\mathit {dc}}}$এবং ${\displaystyle b\mathrm {=} {\mathit {ec}}}$(যেখানে d, e যেকোন সংখ্যা)।

তাহলে বলা যায়, c প্রথম ভাগশেষ ${\displaystyle {r}_{0}}$ কে নিঃশেষে ভাগ করে কারণ, ${\displaystyle {r}_{0}\mathrm {=} a\mathrm {-} {\mathit {bq}}_{0}\mathrm {=} {\mathit {dc}}\mathrm {-} {\mathit {ecq}}_{0}\mathrm {=} \left(d\mathrm {-} {\mathit {eq}}_{0}\right)c}$

একি ভাবে দেখানো যায় c সব ${\displaystyle {r}_{x}}$ কেই নিঃশেষে ভাগ করে, যেমন ${\displaystyle {r}_{1}\mathrm {=} b\mathrm {-} {r}_{0}{q}_{1}\mathrm {=} {\mathit {ec}}\mathrm {-} \left(d\mathrm {-} {\mathit {eq}}_{0}\right){\mathit {cq}}_{1}\mathrm {=} \left(e\mathrm {-} \left(d\mathrm {-} {\mathit {eq}}_{0}\right){q}_{1}\right)c}$

তাই প্রমাণিত হয়, c ${\displaystyle {r}_{n\mathrm {-} 1}}$ কে নিঃশেষে ভাগ করে। যেহেতু ${\displaystyle c\mathrm {=} g}$ হতে পারে সেহেতু বলা যায় ${\displaystyle g}$, ${\displaystyle {r}_{n\mathrm {-} 1}}$ এর গুণনীয়ক। এর মানে ${\displaystyle g\mathrm {\leq } {r}_{n\mathrm {-} 1}}$ হতে হবে।

এই দুই সর্তকে যদি এক সাথে সত্যি হতে হয় তাহলে নিশ্চিত ভাবে বলা যায়, ${\displaystyle g\mathrm {=} {r}_{n\mathrm {-} 1}}$। অর্থাৎ ভাগ প্রক্রিয়ার সত্যতা প্রমাণিত হলো।