ক্রিস-ক্রস এ্যালগোরিদম
ক্রিস-ক্রস এ্যালগোরিদম গাণিতিক সমস্যা সমাধানের জন্য লিনিয়ার প্রোগ্রামিং-এ ব্যবহৃত্ একটি পদ্ধতি।
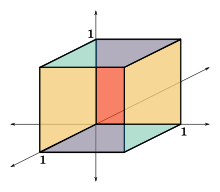
ক্রিস-ক্রস এ্যালগোরিদম সবচেয়ে জটিল আবস্তায় ক্লি-মিন্টি ঘনকের ৮টি কোণেই প্রতিটিই পরিভ্রমণ করে। এটি গড়ে ৩টি আতিরিক্ত কোণে যায়। এখানে ক্লি-মিন্টি ঘনকের একটি কৌণিক দৃশ্য দেখানো হলো।
ইতিহাস
ক্রিস-ক্রস এ্যালগোরিদম টামাস টার্লাকি[1] এবং ঝি-মিন[2] কর্তৃক পৃথকভাবে প্রকাশিত হয়; তবে এই এ্যালগোরিদিমটি অন্যান্য আরো কয়েকজন গবেষকের অপ্রকাশিত প্রতিবেদনেও উল্লেখ ছিলো।[3]
আরও দেখুন
- জ্যাক এডমুন্ডস
তথ্যসূত্র
- Avis, David; Fukuda, Komei (ডিসেম্বর ১৯৯২)। "A pivoting algorithm for convex hulls and vertex enumeration of arrangements and polyhedra"। Discrete and Computational Geometry। 8 (ACM Symposium on Computational Geometry (North Conway, NH, 1991) number 1): 295–313। doi:10.1007/BF02293050। এমআর 1174359।
- Csizmadia, Zsolt; Illés, Tibor (২০০৬)। "New criss-cross type algorithms for linear complementarity problems with sufficient matrices" (pdf)। Optimization Methods and Software। 21 (2): 247–266। doi:10.1080/10556780500095009। এমআর 2195759।
- Fukuda, Komei; Namiki, Makoto (মার্চ ১৯৯৪)। "On extremal behaviors of Murty's least index method"। Mathematical Programming। 64 (1): 365–370। doi:10.1007/BF01582581। এমআর 1286455।
- Fukuda, Komei; Terlaky, Tamás (১৯৯৭)। Liebling, Thomas M.; de Werra, Dominique, সম্পাদকগণ। "Criss-cross methods: A fresh view on pivot algorithms"। Mathematical Programming: Series B। Amsterdam: North-Holland Publishing Co.। 79 (Papers from the 16th International Symposium on Mathematical Programming held in Lausanne, 1997, number 1–3): 369–395। doi:10.1007/BF02614325। এমআর 1464775। Postscript preprint।
- den Hertog, D.; Roos, C.; Terlaky, T. (১ জুলাই ১৯৯৩)। "The linear complementarity problem, sufficient matrices, and the criss-cross method" (pdf)। Linear Algebra and its Applications। 187: 1–14। doi:10.1016/0024-3795(93)90124-7। এমআর 1221693।
- Illés, Tibor; Szirmai, Ákos; Terlaky, Tamás (১৯৯৯)। "The finite criss-cross method for hyperbolic programming"। European Journal of Operational Research। 114 (1): 198–214। doi:10.1016/S0377-2217(98)00049-6। Zbl 0953.90055। Postscript preprint।
- Klafszky, Emil; Terlaky, Tamás (জুন ১৯৯১)। "The role of pivoting in proving some fundamental theorems of linear algebra" (postscript)। Linear Algebra and its Applications। 151: 97–118। doi:10.1016/0024-3795(91)90356-2। এমআর 1102142।
- Roos, C. (১৯৯০)। "An exponential example for Terlaky's pivoting rule for the criss-cross simplex method"। Mathematical Programming। Series A। 46 (1): 79–84। doi:10.1007/BF01585729। এমআর 1045573।
- Terlaky, T. (১৯৮৫)। "A convergent criss-cross method"। Optimization: A Journal of Mathematical Programming and Operations Research। 16 (5): 683–690। doi:10.1080/02331938508843067। আইএসএসএন 0233-1934। এমআর 0798939।
- Terlaky, Tamás (১৯৮৭)। "A finite crisscross method for oriented matroids"। Journal of Combinatorial Theory। Series B। 42 (3): 319–327। doi:10.1016/0095-8956(87)90049-9। আইএসএসএন 0095-8956। এমআর 0888684।
- Terlaky, Tamás; Zhang, Shu Zhong (১৯৯৩) [1991]। "Pivot rules for linear programming: A Survey on recent theoretical developments"। Annals of Operations Research। Springer Netherlands। 46–47 (Degeneracy in optimization problems, number 1): 203–233। doi:10.1007/BF02096264। আইএসএসএন 0254-5330। এমআর 1260019। টেমপ্লেট:Citeseerx।
- Wang, Zhe Min (১৯৮৭)। "A finite conformal-elimination free algorithm over oriented matroid programming"। Chinese Annals of Mathematics (Shuxue Niankan B Ji)। Series B। 8 (1): 120–125। আইএসএসএন 0252-9599। এমআর 0886756।
বহি:সংযোগ
- Komei Fukuda (ETH Zentrum, Zurich) with publications
- Tamás Terlaky (Lehigh University) with publications
টেমপ্লেট:Mathematical programming টেমপ্লেট:Optimization algorithms
This article is issued from
Wikipedia.
The text is licensed under Creative
Commons - Attribution - Sharealike.
Additional terms may apply for the media files.