মৌলিক সংখ্যা উপপাদ্য

সংখ্যাতত্ত্বে মৌলিক সংখ্যা উপপাদ্য (ইংরেজি ভাষায়: Prime number theorem সংক্ষেপে PNT) মৌলিক সংখ্যাসমূহের আসন্ন, অসীমতটীয় বিন্যাস ব্যাখ্যা করে। সংখ্যা যত বড় হয়, মৌলিক সংখ্যার পরিমাণ তত কমে আসে। এই কমে আসার প্রকৃতি কী রকম, মৌলিক সংখ্যা উপপাদ্য তার নির্ভুল বর্ণনা দেয়।

সাধারণভাবে, মৌলিক সংখ্যা উপপাদ্য বলে যে যদি আমরা কোন বড় সংখ্যা N-এর কাছাকাছি কোন সংখ্যা দৈব চয়ন করি, তবে সংখ্যাটির একটি মৌলিক সংখ্যা হবার সম্ভাবনা প্রায় 1 / ln(N), যেখানে ln(N) হল N-এর স্বাভাবিক লগারিদম। উদাহরণস্বরূপ। যখন N = ১০,০০০, এর আশেপাশে প্রতি ৯টি সংখ্যার ১টি মৌলিক, অন্যদিকে যখন N = ১,০০০,০০০,০০০, কেবল তার আশেপাশের ২১টি সংখ্যার একটি মৌলিক।

উপপাদ্যের বিবৃতি

Graph comparing π(x), x / ln x and Li(x)

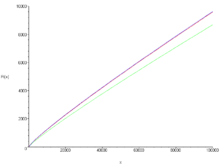
ধরি π(x) হচ্ছে মৌলিক সংখ্যা গণনাকারী ফাংশন যা কোন স্বাভাবিক সংখ্যা x-এর সমান বা ছোট মানের মৌলিক সংখ্যার সংখ্যা প্রদান করে। উদাহরণস্বরূপ, π(10) = 4 কারণ চারটি মৌলিক সংখ্যা আছে (২, ৩, ৫ ও ৭) যেগুলি ১০-এর সমান বা ছোট। মৌলিক সংখ্যা উপপাদ্য বলে যে, যদি x-এর মান অসীমের নিকটবর্তী হয়, তবে π(x) এবং x / ln(x) ফাংশনদ্বয়ের ভাগফলের সীমা ১। সূত্র আকারে:

\lim _{x\to \infty }{\frac {\pi (x)}{x/\ln(x)}}=1,

এটি মৌলিক সংখ্যাসমূহের বিন্যাসের অসীমতটীয় বিধি (the asymptotic law of distribution of prime numbers) নামে পরিচিত।

এ সম্বন্ধে একটি তালিকা

x	π(x)	π(x) - x / ln(x)	π(x) / ( x / ln(x) )	li(x) - π(x)	li(x) / π(x)	x / π(x)
10⁰=1	0	অসংজ্ঞাত ln(1)=0	অসংজ্ঞাত ln(1)=0	-অসীম	অসংজ্ঞাত	অসংজ্ঞাত
2	1	-2	0,347	0	0	2,000
4	2	-1	0,693	1	1,500 000 000 000	2,000
10¹	4	-0	0,921	2	1,500 000 000 000	2,500
10²	25	3	1,151	5	1,200 000 000 000	4,000
10³	168	23	1,161	10	1,059 523 809 524	5,952
10⁴	1 229	143	1,132	17	1,013 832 384 052	8,137
10⁵	9 592	906	1,104	38	1,003 961 634 696	10,430
10⁶	78 498	6 116	1,084	130	1,001 656 093 149	12,740
10⁷	664 579	44 159	1,071	339	1,000 510 097 370	15,050
10⁸	5 761 455	332 774	1,061	754	1,000 130 869 720	17,360
10⁹	50 847 534	2 592 592	1,054	1 701	1,000 033 452 950	19,670
10¹⁰	455 052 511	20 758 029	1,048	3 104	1,000 006 821 191	21,980
10¹¹	4 118 054 813	169 923 159	1,043	11 588	1,000 002 813 950	24,280
10¹²	37 607 912 018	1 416 705 193	1,039	38 263	1,000 001 017 419	26,590
10¹³	346 065 536 839	11 992 858 452	1,034	108 971	1,000 000 314 885	28,900
10¹⁴	3 204 941 750 802	102 838 308 636	1,033	314 890	1,000 000 098 251	31,200
10¹⁵	29 844 570 422 669	891 604 962 452	1,031	1 052 619	1,000 000 035 270	33,510
10¹⁶	279 238 341 033 925	7 804 289 844 392	1,029	3 214 632	1,000 000 011 512	35,810
4.10¹⁶	1 075 292 778 753 150	28 929 900 579 949	1,028	5 538 861	1,000 000 005 151	37,200
10¹⁷	2 623 557 157 654 233	68 883 734 693 281	1,027	7 956 589	1,000 000 003 033	38,116
10¹⁸	24 739 954 287 740 860	612 483 070 893 536	1,025	21 949 555	1,000 000 000 887	40,420
10¹⁹	234 057 667 276 344 607	5 481 624 169 369 960	1,024	99 877 775	1,000 000 000 427	42,725
10²⁰	2 220 819 602 560 918 840	49 347 193 044 659 701	1,023	222 744 644	1,000 000 000 100	45,028
10²¹	21 127 269 486 018 731 928	446 579 871 578 168 707	1,022	597 394 254	1,000 000 000 028	47,332
10²²	201 467 286 689 315 906 290	4 060 704 006 019 620 994	1,021	1 932 355 208	1,000 000 000 010	49,636
10²³	1 925 320 391 606 803 968 923	37 083 513 766 578 631 309	1,020	7 250 186 216	1,000 000 000 004	51,939

অন্যভাবে, মৌলিক সংখ্যা উপপাদ্য বলে যে n-তম মৌলিক সংখ্যা π_n এবং n ln(n) প্রায় সমান, এবং n যত অসীমের দিকে অগ্রসর হয়, এই আসন্ন মানে ভুলের পরিমাণ ততই শূন্যের দিকে অগ্রসর হয়।

আরও দেখুন

মৌলিক সংখ্যা গণনাকারী ফাংশন

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.