வட்டத்தைச் சதுரமாக்கல்

வட்டத்தைச் சதுரமாக்கல் (squaring the circle) என்பது பண்டைய கணிதவியலாளர்கள்]] முன்மொழிந்த ஒரு கணிதச் சிக்கல் ஆகும். இது குறிப்பிட்ட படிநிலைகளில் கவராயத்தையும் நேர்விளிம்பையும் பயன்படுத்தி, வட்டத்தின் பரப்புக்குச் சமமான பரப்புடைய சதுரத்தை வரையும் அறைகூவலாகும். இதை மேலும் நுண்ணிலையாகவும் மேலும் துல்லியமாகவும் கூறவேண்டுமென்றால், கோடுகள், வட்டங்கள் நிலவல் சார்ந்த குறிப்பிட்ட யூக்ளீடிய அடிக்கோள்களால் இத்தகு சதுரம் நிலவலை உறுதிப்படுத்தமுடியுமா என வினவலுக்குச் சமமாகும்.

வட்டத்தைச் சதுரமாக்கல்: சதுரப் பரப்பும் வட்டப் பரப்பும் π மதிப்புக்குச் சமமாக வேண்டும். குறிப்பிட்ட படிநிலைகளில் கவராயத்தையும் நேர்விளிம்பையும் பயன்படுத்தி இவ்வட்டத்தை வரைய முடியாதென 1882 இல் நிறுவப்பட்டது.

சில தோராயப் பொய்யான தீர்வுகள் நெடுங்காலமாக நம்பப்பட்டு வந்தன. உருவத்தில் உள்ள கோடிட்ட பகுதி இப்பொக்க்ரேட்டசின் பிறை ஆகும். இப்பரப்பு (சியோசின் இப்பொக்கிரேட்டெசு கண்டறிந்தபடி), ABC முக்கோணப் பரப்புக்குச் சமமாகும்.

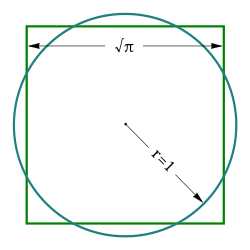
இது இயலாதென 1882இல் இலிண்டேமன்–வியெர்சுடிராசு தேற்றம் வாயிலாக நிறுவப்பட்டது. பை (கணித மாறிலி) (π) ஒரு இயற்கணித விகிதமுறா எண் என்பதைவிட அது ஒரு கடந்தநிலை எண் என இத்தேற்றம் கூறுகிறது. அதாவது, இது விகிதமுறு எண் கெழுக்களால் அமைந்த பல்லுறுப்புக்கோவைச் சார்பொன்றின் மூலமாக (Root) அமையமுடியாது என்கிறது. ஏற்கெனவே 1882இற்கு முன் பல பத்தாண்டுகளாகவே Pi ஒரு கடந்தநிலை எண்ணாக இருந்தால் வட்டத்தைச் சதுரமாக்கல் இயலாதெனக் கூறப்பட்டும் நம்பப்பட்டும் வந்தது. π மதிப்புக்கு அருகில் பகு எண்கள் உள்ளமையால், மாறாக, முழுநிறைவற்ற துல்லிய மதிப்புடைய தோராயச் சதுரமாக்கல் இயல்வதே.

வட்டத்தைச் சதுரமாக்கல் எனும் கோவை இயலாததைச் செய்யமுனையும் செயலுக்கு உருவகமாகவும் சிலவேளைகளில் பயன்படுத்தப்படுகிறது.[1]

வட்டத்தைச் சதுரமாக்கல் எனும் பொருளில் சிலவேளைகளில் வட்டத்தின் இருபடியாக்கல் எனும் கோவை பயன்படுத்தப்படுகிறது. ஆனால் இதுவும் வட்டப் பரப்பைக் கண்டறிவதற்கான தோராயமான எண்ணியல் முறைகளையே குறிக்கும்.