போலி (கணிதம்)

பின்வரும் எடுத்துக்காட்டில் சுழியால் வகுத்தலைப் பயன்படுத்தி ${\displaystyle 2=1}$ எனக் காட்டப்பட்டுள்ளது. இந்தப் போலியிலே மாற்றம் செய்வதன் மூலம் எந்தவோர் எண்ணும் மற்ற எந்தவோர் எண்ணுக்கும் சமன் எனக் காட்டலாம்.

1. ${\displaystyle a}$உம் ${\displaystyle b}$உம் சமனாகும். ${\displaystyle a\neq 0}$, ${\displaystyle b\neq 0}$

${\displaystyle a=b\,}$

2. இரு பக்கங்களையும் ${\displaystyle a}$ஆல் பெருக்குக.

${\displaystyle a^{2}=ab\,}$

3. ${\displaystyle b^{2}}$ஐக் கழிக்குக.

${\displaystyle a^{2}-b^{2}=ab-b^{2}\,}$

4. இரு பக்கங்களையும் காரணியாக்குக.

${\displaystyle (a-b)(a+b)=b(a-b)\,}$

5. ${\displaystyle (a-b)}$ஆல் வகுக்குக.

${\displaystyle a+b=b\,}$

6. ${\displaystyle a=b}$ என்பதால்,

${\displaystyle b+b=b\,}$

7. ${\displaystyle b}$ஐயும் ${\displaystyle b}$ஐயும் கூட்டுக.

${\displaystyle 2b=b\,}$

8. சுழியல்லாத ${\displaystyle b}$ஆல் வகுக்குக.

${\displaystyle 2=1\,}$[4]

இங்கே போலி ஐந்தாவது வரியில் உள்ளது. ஐந்தாவது வரியில் சமன்பாடு ${\displaystyle (a-b)}$ஆல் வகுக்கப்படுகின்றது. ஆனால், ${\displaystyle a=b}$ என்பதால் ${\displaystyle a-b=0}$ ஆகும். சுழியால் வகுக்கும்போது கிடைக்கும் பெறுமானத்தைத் தீர்மானிக்க முடியாது என்பதால் மேற்கூறிய நிறுவல் தவறாகும்.

${\displaystyle 2\times 0=1\times 0}$ எனும் சமன்பாட்டில் (இது உண்மையானது!) இரு பக்கங்களிலும் சுழியால் வகுப்பதன் மூலம் ${\displaystyle 1=2}$ எனக் காட்டுவதும் இவ்வாறே தவறாகும். இதுவும் ஒரு போலியே.

${\displaystyle 1={\sqrt {1}}={\sqrt {(-1)(-1)}}={\sqrt {-1}}{\sqrt {-1}}=i\cdot i=-1}$

${\displaystyle {\sqrt {xy}}={\sqrt {x}}{\sqrt {y}}}$ என்பது ${\displaystyle x}$, ${\displaystyle y}$ என்பனவற்றில் ஏதேனும் ஓரெண்ணாவது நேர் எண்ணாக இருந்தால் மட்டுமே ஏற்றுக்கொள்ளக்கூடியதாகும். இங்கே அவ்வாறான போலியே நிகழ்ந்துள்ளது.

நிறுவலுக்கான படம்

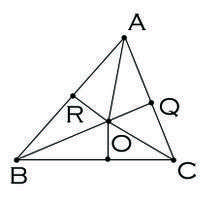
பின்வரும் ஏற்றுக்கொள்ளப்பட முடியாத நிறுவலானது எந்தவொரு முக்கோணியுமே இருசமபக்க முக்கோணி தான் எனக் கூறுகின்றது.

தரப்பட்ட △ABCஇல் AB=AC என நிறுவுக.

1. ∠Aஇன் கோண இருகூறாக்கியை வரைக.
2. BCஇன் நடுப்புள்ளியை D எனப் பெயரிடுக.
3. D ஒரு புள்ளியாகவுள்ள BCஇன் செங்குத்து இருசமகூறாக்கியை வரைக.
4. மேற்கூறிய இரு கோடுகளும் சமாந்தரமெனின், AB = AC; அல்லாவிடின், அவை Oஇல் சந்திக்கும்.
5. ABஇற்குச் செங்குத்தாக ORஐயும் ACஇற்குச் செங்குத்தாக OQஐயும் வரைக.
6. நேர்கோடுகள் OBஐயும் OCஐயும் வரைக.
7. △RAO ≅ △QAO (AO = AO; ∠OAQ ≅ ∠OAR. ஏனெனில், AOஆனது ∠Aஐ இருசமகூறாக்குகின்றது; ∠ARO ≅ ∠AQO. ஏனெனில், அவரை இரண்டும் செங்கோணங்கள்.)
8. △ODB ≅ △ODC (∠ODB, ∠ODC ஆகிய இரண்டும் செங்கோணங்கள்; OD = OD; BD = CD. ஏனெனில் ODஆனது BCஐ இருசமகூறாக்குகின்றது.)
9. △ROB ≅ △QOC (RO = QO. ஏனெனில், △RAO ≅ △QAO; BO = CO. ஏனெனில், △ODB ≅ △ODC; ∠ORBஉம் ∠OQCஉம் செங்கோணங்கள்.)
10. ஆகவே, AR ≅ AQ, RB ≅ QC, AB = AR + RB = AQ + QC = AC

மேற்கூறிய முறையின்படி AB = AC என்றும் AC = BC என்றும் காட்டுவதன் மூலம் அனைத்து முக்கோணிகளுமே சமமானவை எனவும் காட்ட முடியும்.

ஆனாலும் போலி படத்திலேயே உள்ளது. AB ≠ AC ஆக இருப்பின், Oஆனது முக்கோணிக்கு உள்ளே அமைந்திருக்காது. முக்கோணிக்கு வெளியேயே அமைந்திருக்கும். ABஆனது ACஐ விட நீளம் கூடியதாக இருப்பின், Rஆனது ABஇனுள்ளும் Qஆனதும் ACஇற்கு வெளியேயும் (அல்லது மறுதலையாக) அமைந்திருக்கும். துல்லியமான கணித உபகரணங்களின் மூலம் வரையப்பட்ட படம் மேற்கூறிய இரண்டையும் உறுதிப்படுத்தும். இதன் காரணமாக, AB = AR + RB எனவே அமைந்திருக்கும். ஆனால், ACஆனது AQ - QC என்பதற்குச் சமனாக இருக்கும். ஆகவே, அவ்விரு நீளங்களும் சமனல்லவே.