பிரம்ம குப்தரின் தேற்றம்
வடிவவியலில் பிரம்ம குப்தரின் தேற்றம் என்பது ஒரு வட்ட நாற்கரத்தைப்பற்றி ஓர் உண்மையைக் கூறுவது. தேற்றம் கூறும் உண்மை: ஒரு வட்ட நாற்கரத்தின் மூலைவிட்டங்கள் செங்குத்தாக வெட்டினால், அந்த நாற்கரத்தின் பக்கத்தின் செங்குத்துக்கோடு மூலைவிட்டங்கள் வெட்டும் புள்ளி வழியாகச் சென்றால், அக்கோடு அந்த நாற்கரத்தின் எதிர்ப்பக்கத்தை இரு சரிபாதியாக வெட்டும்.
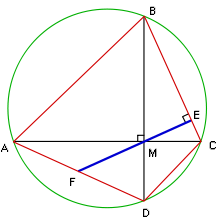
குறிப்பாக A, B, C ,D என்பனவற்றை வட்ட நாற்கரத்தின் நான்கு மூலைகளாகக் கொண்டால், மூலை விட்டங்களாகிய AC -உம் BD -உம் ஒன்றை ஒன்று செங்குத்தாக வெட்டும். வெட்டும் புள்ளியை M என்போம். இப்பொழுது M என்னும் புள்ளியில் இருந்து BC என்னும் பக்கத்துக்கு ஓர் செங்குத்துக்கோடு வரைவோம். அது BC பக்கத்தில் முட்டும் இடத்தை E என்போம். இந்த EM என்னும் கோட்டை நீட்டினால் அது எதிர்ப்புறம் உள்ள நாற்கரத்தின் AD என்னும் பக்கத்தை F என்னும் புள்ளியில் வெட்டும் (அல்லது முட்டும்). இப்பொழுது இந்தத் தேற்றம் என்ன சொல்கின்றது என்றால், F என்பது AD என்னும் பக்கத்தின் நடுப்புள்ளி (அதாவது F என்பது AD என்னும் பக்கத்தை இரு சரிபாதிகளாகப் (சரிசமமாகப்) பிரிக்கின்றது .
நிறுவல்

நாம் என்ன நிறுவ வேண்டும் என்றால், AF = FD என்று நிறுவ வேண்டும். நாம் AF -உம் FD -உம் FM உக்கு ஈடு அல்லது சமம் என்று நிறுவுவோம் .
உண்மையில் AF = FM என்று நிறுவ, முதலில் கோணங்கள் FAM -உம் CBM ஈடு அல்லது சமம் என்னும் உண்மையைக் கொள்ளுவோம், ஏனெனில் அவை மூலைதொடு வட்டத்தின் ஒரே வட்டப் பகுதியின் ("DC" என்னும் பகுதியின்) கோணங்கள். மேலும் கோணங்கள் CBM உம் CME உம் ஆகிய இரண்டும் BCM இன் நிரப்புக் கோணங்கள் (சேர்த்தால் 90° கிட்டும்), ஆகவே அவை சமமானவை. கடைசியாக கோணங்கள் CME உம் FMA உம் சமம். எனவே AFM என்பது இருசமபக்க முக்கோணம் , எனவே பக்கங்கள் AF உம் FM உம் சமம். AF = FM
இதே போலவே FD = FM என்பதன் நிறுவலும் செய்யலாம், கோணங்கள் FDM, BCM, BME, DMF ஆகியவை எல்லாம் சமம், ஆகவே DFM என்பது இருசமபக்க முக்கோணம். எனவே FD = FM. இதில் இருந்து AF = FD என்பது உறுதியாகின்றது. எனவே தேற்றம் கூறுவது உண்மை.
வெளியிணைப்புகள்
- Weisstein, Eric W., "Brahmagupta's theorem", MathWorld.
- Brahmagupta's Theorem at cut-the-knot