சார்பின் மூலம்

கணிதத்தில் ஒரு மெய்மதிப்பு அல்லது சிக்கலெண்மதிப்பு அல்லது திசையன்மதிப்புச் சார்புபொன்றின் ஆட்களத்தில் உள்ள ஒரு உறுப்பின் சார்பலன் சுழியாக இருந்தால், அந்த உறுப்பானது அச் சார்பின் மூலம் அல்லது சார்பின் சுழியம் (zero of a function அல்லது root of a function) எனப்படுகிறது.

${\displaystyle \scriptstyle {[-2\pi ,2\pi ]}}$ ஆட்களத்தில் சார்பு cos(x) இன் வரைபடம். x இன் ${\displaystyle \scriptstyle {\frac {-3\pi }{2}}}$, ${\displaystyle \scriptstyle {\frac {-\pi }{2}}}$, ${\displaystyle \scriptstyle {\frac {\pi }{2}}}$ and ${\displaystyle \scriptstyle {\frac {3\pi }{2}}}$ மதிப்புகள் சார்பின் மூலங்கள் (சிவப்பு).

சார்பு f இன் ஆட்களத்தின் ஒரு உறுப்பு x இச் சார்பின் மூலம் எனில்,

${\displaystyle f(x)=0\,}$ ஆகும்.

சுழி (0) வெளியீட்டைத் தருகின்ற உள்ளீடாகவும் சார்பின் மூலத்தைக் கூறலாம்.[1]

ஒரு பல்லுறுப்புக்கோவையின் மூலம் என்பது அக் கோவைக்குரியச் சார்பின் மூலமாகும். இயற்கணிதத்தின் அடிப்படைத் தேற்றத்தின்படி ஒரு சுழியற்ற பல்லுறுப்புக்கோவையின் மூலங்களின் எண்ணிக்கை அக் கோவையின் படிக்குச் சமமானதாக இருக்கும்.

எடுத்துக்காட்டு:

${\displaystyle f(x)=x^{2}-5x+6}$ இன் படி 2. மேலும் இப்பல்லுறுப்புக்கோவையின் இரு மூலங்கள் 2, 3

${\displaystyle f(2)=2^{2}-5\cdot 2+6=0,\quad f(3)=3^{2}-5\cdot 3+6=0}$

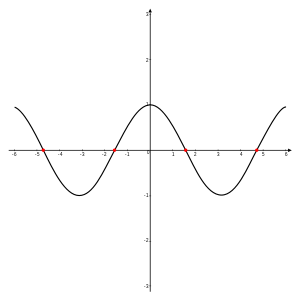
மெய்யெண்கணத்திலிருந்து மெய்யெண்கணத்திற்கு ஒரு சார்பு வரையறுக்கப்படும் போது, அச் சார்பின் வரைபடம் x-அச்சைச் சந்திக்கும் புள்ளிகளின் x-ஆய தொலைவுகள் சார்பின் மூலங்களாக இருக்கும்.