ஆய்லர் கோடு
வடிவியலில் சமபக்க முக்கோணமாக இல்லாத எந்தவொரு முக்கோணத்திற்கும் அதன் நடுக்கோட்டுச் சந்தி, செங்குத்துச்சந்தி, சுற்றுவட்ட மையம் மற்றும் ஒன்பது புள்ளி வட்டமையம் ஆகிய நான்கு புள்ளிகளும் ஒரே கோட்டின் மீது அமையும். இக்கோடு, கணிதவியலாளர் லியோனார்டு ஆய்லரின் பெயரால் ஆய்லர் கோடு (Euler line) என அழைக்கப்படுகிறது.
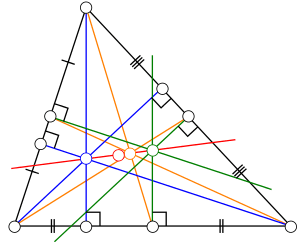
1765 -ல் ஆய்லர் எந்தவொரு முக்கோணத்திலும் அதன் செங்கோட்டு மையம், சுற்றுவட்ட மையம் மற்றும் நடுக்கோட்டுச் சந்தி ஆகிய மூன்றும் ஒருகோட்டுப் புள்ளிகளாக அமையும் என்பதைக் கண்டுபிடித்தார். அக்கோட்டின் மீது ஒன்பது புள்ளி வட்டமையமும் அமையும் என்பது ஆய்லர் காலத்தில் கண்டறிந்திருக்கப்படவில்லை. சமபக்க முக்கோணத்தில் இந்நான்கு புள்ளிகளும் ஒரே புள்ளியாக இருக்கும். மற்ற முக்கோணங்களில், அவை வெவ்வேறான புள்ளிகளாகவும் ஆய்லர் கோடு இவற்றில் ஏதேனும் இரு புள்ளிகளால் தீர்மானிக்கப்படும் கோடாகவும் அமையும். ஆய்லர் கோட்டின் மீது ஒன்பது புள்ளி வட்டமையமானது செங்கோட்டு மையத்திற்கும் சுற்றுவட்ட மையத்திற்கும் இடையே அமையும். மேலும் நடுக்கோட்டுச் சந்திக்கும் சுற்றுவட்ட மையத்திற்கும் இடையே உள்ள தூரமானது, நடுக்கோட்டுச் சந்திக்கும் செங்கோட்டுச்சந்திக்கும் இடையே உள்ள தூரத்தில் பாதியளவாக இருக்கும்.
இரு சமபக்க முக்கோணத்திற்கு மட்டும் உள்வட்ட மையமும் ஆய்லர் கோட்டின் மீது அமையும்.
A, B, C – எடுத்துக்கொண்ட முக்கோணத்தின் உச்சிகள் மற்றும் x : y : z, முந்நேரியல் ஆயதொலைவுகளில் ஒரு மாறும் புள்ளி எனில் ஆய்லர் கோட்டின் சமன்பாடு :
துணையலகு t மூலமாக ஆய்லரின் கோடு:
சுற்றுவட்ட மையம் (முந்நேரியல் ஆயதொலைவுகளில்: ) மற்றும் செங்கோட்டு மையம் (முந்நேரியல் ஆயதொலைவுகளில்: ) தொடங்கி ஆய்லர் கோட்டின் மீதமையும் ஒவ்வொரு புள்ளியும் (செங்கோட்டு மையம் நீங்கலாக) கீழுள்ளவாறு தரப்படுகிறது:
எடுத்துக்காட்டு:
- நடுக்கோட்டுச் சந்தி =
- ஒன்பது புள்ளி வட்டமையம் =
- டீ லாங்சாம்ஸ் (De Longchamps) புள்ளி =
- ஆய்லர் முடிவிலி புள்ளி =
மேற்கோள்கள்
- Leonhard Euler (1767). "Solutio facilis problematum quorundam geometricorum difficillimorum". Novi Commentarii academiae scientarum imperialis Petropolitanae 11: 103–123. E325. http://math.dartmouth.edu/~euler/pages/E325.html. Reprinted in Opera Omnia, ser. I, vol. XXVI, pp. 139–157, Societas Scientiarum Naturalium Helveticae, Lausanne, 1953, வார்ப்புரு:MR.
- Kimberling, Clark (1998). "Triangle centers and central triangles". Congressus Numerantium 129: i–xxv, 1–295.
வெளி இணைப்புகள்
- Altitudes and the Euler Line and Euler Line and 9-Point Circle at cut-the-knot
- Triangle centers on the Euler line, by Clark Kimberling.
- An interactive applet showing several triangle centers that lies on the Euler line.
- Eric W. Weisstein, Euler Line MathWorld இல்.
- "Euler Line" by Eric Rowland, the Wolfram Demonstrations Project, 2007.
- Nine-point conic and Euler line generalization at Dynamic Geometry Sketches Generalizes nine-point circle to a nine-point conic with an associated generalization of the Euler line.