ஆடமார்டு பெருக்கல் (அணிகள்)
கணிதத்தில் ஆடமார்டு பெருக்கல் (Hadamard product) அல்லது உறுப்புவாரிப் பெருக்கல் (entrywise product)[1]) என்பது இரு அணிகளுக்கிடையான ஈருறுப்புச் செயலியாகும். இதில் சமவரிசையுள்ள இரு அணிகளைக் கொண்டு மற்றொரு புது அணி உருவாக்கப்படுகிறது. இரு அணிகளில், ஒரு அணியின் உறுப்பு ஒவ்வொன்றையும் அதற்கு ஒத்த இடத்தில் இரண்டாவது அணியில் உள்ள உறுப்புடன் பெருக்கிக் கிடைக்கும் விடையானது புது அணியின் அதே ஒத்த உறுப்பாக எழுதிக் கொள்ளப்படும். அதாவது, ஒரு அணியின் ij உறுப்பானது மற்றதன் ij உறுப்புடன் பெருக்கக்கிடைக்கும் விடையானது புது அணியின் ij உறுப்பாக எழுதப்படுகிறது. பொதுவான அணிப்பெருக்கலில் இருந்து இச்செயல் மாறுபட்ட ஒன்றாகும்.
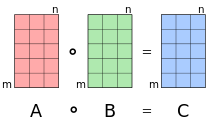
இச்செயல் சேர்ப்புப் பண்பும் பங்கீட்டுப் பண்பும் உடையது. அணிப்பெருக்கலைப் போலில்லாமல் இப்பெருக்கல் பரிமாற்றுத்தன்மையும் கொண்டது.
வரையறை
இரண்டும் வரிசை அணிகள் எனில் அவற்றின் ஆடமார்டு பெருக்கல் அணியான ஒரு வரிசை அணியாக இருக்கும். அதன் உறுப்புகள் கீழுள்ளவையாக இருக்கும்:
- .
இன் வரிசை , இன் வரிசை ஆகவும், , இரண்டும் உண்மையாகவோ அல்லது ஏதேனுமொன்று உண்மையாகவோ இருந்தால் அணிகளின் ஆடமார்டு பெருக்கலை ( ) வரையறுக்க முடியாது.
எடுத்துக்காட்டு
3×3 வரிசை அணிகள் A , B இன் ஆடமார்டு பெருக்கல்:
பண்புகள்
- ஆடமார்டு பெருக்கல் பரிமாற்றுத்தன்மை, சேர்ப்புப் பண்பு, கூட்டல் மீதான பங்கீட்டுப் பண்பு உடையது:
- ஆடமார்டு பெருக்கலின் கீழ், இரு m x n அணிகளின் முற்றொருமை அணியானது அனைத்து உறுப்புகளும் 1 ஆகவுள்ள m x n அணியாக இருக்கும். இவ்வணியானது, வழமையான அணிப்பெருக்கலின் கீழ் அமையும் முற்றொருமை அணியிலிருந்து வேறுபட்டதாகும்.
- அனைத்து உறுப்புகளும் பூச்சியமற்றதாக இருந்தால், இருந்தால் மட்டுமே ஒரு அணிக்கு ஆடமார்டு பெருக்கலின் கீழ் நேர்மாறு இருக்கும்.[2]
- , இரு திசையன்கள்; திசையனை முதன்மை மூலைவிட்டமாகக் கொண்ட மூலைவிட்ட அணி திசையனை முதன்மை மூலைவிட்டமாகக் கொண்ட மூலைவிட்ட அணி எனில் பின்வரும் முடிவு உண்மையாகும்:[3]
- , இதில் என்பது இன் இடமாற்று இணையணி ஆகும்.
மேற்கோள்கள்
- (Horn & Johnson 1985, Ch. 5)
- Million, Elizabeth. "The Hadamard Product". பார்த்த நாள் 2 January 2012.
- (Horn & Johnson 1991)
- (Styan 1973)