அறுதி மதிப்புத் தேற்றம்
கணிதத்தில் அறுதி மதிப்புத் தேற்றம் (extreme value theorem) இன் கூற்று:
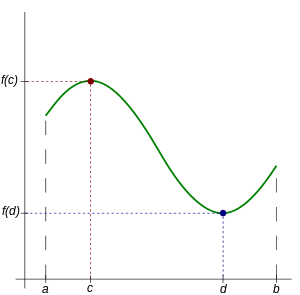
வரம்புடைய மூடிய இடைவெளி [a,b] இல், மெய்மதிப்புச் சார்பு f தொடர்ச்சியானதாக இருந்தால், அந்த இடைவெளிக்குள் குறைந்தது ஒருமுறை அச்சார்பு பெருமம் மற்றும் சிறுமம் அடையும். அதாவது [a,b] இடைவெளிக்குள் கீழ்க்காணுமாறு c , d ஆகிய இரு எண்களைக் காண முடியும்:
இத்தேற்றத்துடன் தொடர்புடைய மற்றொரு தேற்றமான வரம்புடைமைத் தேற்றம் கூற்றின்படி,
மூடிய இடைவெளி [a,b] இல், மெய்மதிப்புச் சார்பு f தொடர்ச்சியானதாக இருந்தால், அந்த இடைவெளிக்குள் கீழ்க்காணுமாறு m , M ஆகிய இரு எண்களைக் காண முடியும்:
அறுதி மதிப்புத் தேற்றம், வரம்புடைமைத் தேற்றத்தின் மேம்பட்ட வடிவாக உள்ளது. வரம்புடைமைத் தேற்றம், சார்பானது வரம்புடையாத அமையும் என்கிறது. ஆனால் அறுதி மதிப்புத் தேற்றம் மேலும் அதிகப்படியாக, சார்பு வரம்புடையதாக மட்டும் இருப்பதோடல்லாது, அதன் குறைந்தபட்ச மேல் வரம்பினைப் பெருமமாகவும், அதிகபட்ச கீழ்வரம்பினைச் சிறுமமாகவும் கொண்டிருக்கும் என்று கூறுகிறது.
அறுதி மதிப்புத் தேற்றம், ரோலின் தேற்றத்தை நிறுவப் பயன்படுத்தப்படுகிறது.
தேற்றம் பயன்படா சார்புகள்
கீழே தரப்பட்டுள்ள எடுத்துக்காட்டுகளிலிருந்து இத் தேற்றத்திற்கு உட்படும் சார்புகளின் ஆட்களங்கள் வரம்புடையவையாகவும் மூடியவையாகவும் இருக்க வேண்டியதின் அவசியத்தைப் புரிந்து கொள்ளலாம்.
- [0, ∞) இடைவெளியில் வரையறுக்கப்பட்ட சார்பு ƒ(x) = x , மேற்புறம் வரம்புடையதாக இல்லை.
- [0, ∞) இடைவெளியில் வரையறுக்கப்பட்ட சார்பு ƒ(x) = x / (1 + x) வரம்புடையது. ஆனால் குறைந்தபட்ச மேல் வரம்பு 1 ஐ அடைவதில்லை.
- (0, 1] இடைவெளியில் வரையறுக்கப்பட்ட சார்பு ƒ(x) = 1 / x மேற்புறம் வரம்புடையதாக இல்லை.
- (0, 1] இடைவெளியில் வரையறுக்கப்பட்ட சார்பு ƒ(x) = 1 – x வரம்புடையது. ஆனால் குறைந்தபட்ச மேல் வரம்பு 1 ஐ அடைவதில்லை.
ƒ(0) = 0 என வரையறுப்பதன் மூலம் அறுதி மதிப்புத் தேற்றம், வரம்புடைமைத் தேற்றம் ஆகிய இரு தேற்றங்களுக்கும், இடைவெளி [a, b] இல் தொடர்ச்சித்தன்மை தேவை என்பதை அறிந்து கொள்ளலாம்.
அரைத் தொடர்ச்சிச் சார்புகளுக்கு நீட்டிப்பு
சார்பு f அரைத் தொடர்ச்சியானதாக இருந்தால் வரம்புடைமைத் தேற்றம் மற்றும் அறுதி மதிப்புத் தேற்றம் இரண்டிலும் அதற்கேற்ற பாதிப்பகுதி உண்மையானதாகும். நீட்டிக்கப்பட்ட மெய்யெண் கோட்டிலிருந்து –∞ அல்லது +∞ மதிப்பைத் தேவைக்கேற்பச் சேர்த்துக் கொள்ளலாம்.
தேற்றம்:
சார்பு f : [a,b] → [–∞,∞) மேல் அரைத் தொடர்ச்சியுடையது எனில்,
- என்றவாறு இருக்கும். அப்போது சார்பு f மேற்புறம் வரம்புடையதாக, குறைந்தபட்ச மேல்வரம்புடன் இருக்கும்.
மேற்கோள்கள்
- Keisler, H. Jerome (1986). Elementary calculus. An infinitesimal approach. Boston, Massachusetts: Prindle, Weber & Schmidt. பன்னாட்டுத் தரப்புத்தக எண்:0-87150-911-3. http://www.math.wisc.edu/~keisler/calc.html.
வெளி இணைப்புகள்
- A Proof for extreme value theorem at cut-the-knot
- Boundedness Theorem பிளாநெட்மேத்தில்
- Extreme Value Theorem பிளாநெட்மேத்தில்
- Extreme Value Theorem by Jacqueline Wandzura with additional contributions by Stephen Wandzura, the Wolfram Demonstrations Project.
- Weisstein, Eric W., "Extreme Value Theorem", MathWorld.